Weighted Interval Scheduling

Problem¹

Instead of just fitting as many tasks like regular interval scheduling problem, we have weight associates with the interval. Now we want to maximize the value.

So basically, $f_i$ finish time sorted in non-decreasing order, $v_i$ is the value, and $s_i$ is the start time. We want $S \subseteq {1… n}$.

We also define $p(j)$ which is the largest i < j which is disjoint(compatible) with j.

Algorithm

Idea:

• Optimal O
  1. $n \in O$, find optimal for {1, p(n)}
  2. $n \notin O$, find optimal {1, n-1}.
• Let $O_j$ = optimal for {1, j}, $OPT(j) = value(O_j)$
• For above two cases then
  1. $OPT(j) = v_j + OPT(p(j))$
  2. $OPT(j) = OPT(j − 1)$
  3. $OPT(j) = max(v_j + OPT(p(j)), OPT(j − 1))$

Calculate the OPT

• Compute-Opt(j)
  • If j=0 then
    • Return 0
  • Else
    • Return max($v_j$+Compute-Opt(p(j)), Compute-Opt(j − 1)) Endif

However, the total numbers will be exponential.

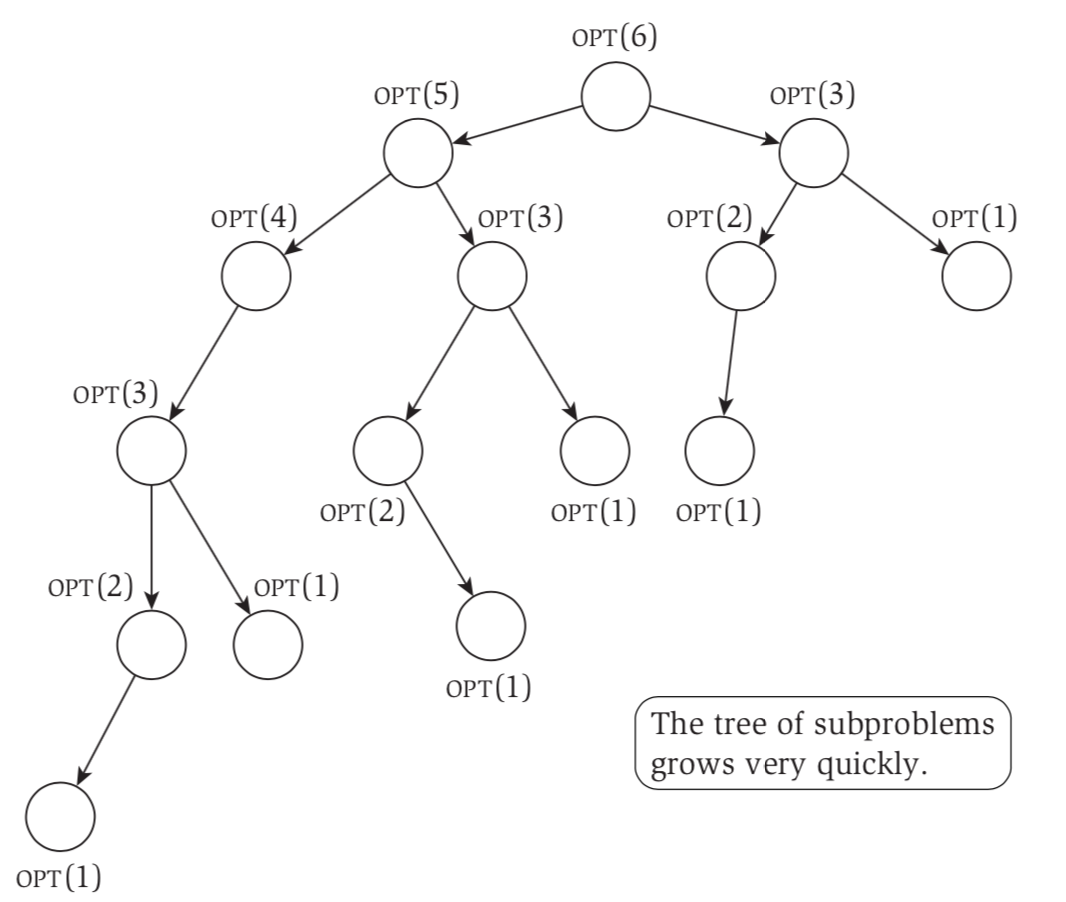
We memoize the intermediate step.

• M-Compute-Opt(j)
  • If j=0 then
    • Return 0
  • Else if M[j] is not empty
    • then Return M[j]
  • Else
    • Define M[j] = max($v_j$+M-Compute-Opt(p(j)), M-Compute-Opt(j − 1))
    • Return M[j]
  • Endif

Retrive Solution

• Find-Solution(j)
  • If j=0 then
    • Output nothing
  • Else
    • If $v_j$+M[p(j)] $\geq$ M[j−1] then
      • Output j together with the result of Find-Solution(p(j))
    • Else
      • Output the result of Find-Solution(j − 1)
    • Endif
  • Endif

Iterative Approach

• Iterative-Compute-Opt
  • M[0]=0
  • For j=1,2,…,n
    • M[j]= max($v_j$ + M[p(j)], M[j − 1])
  • Endfor

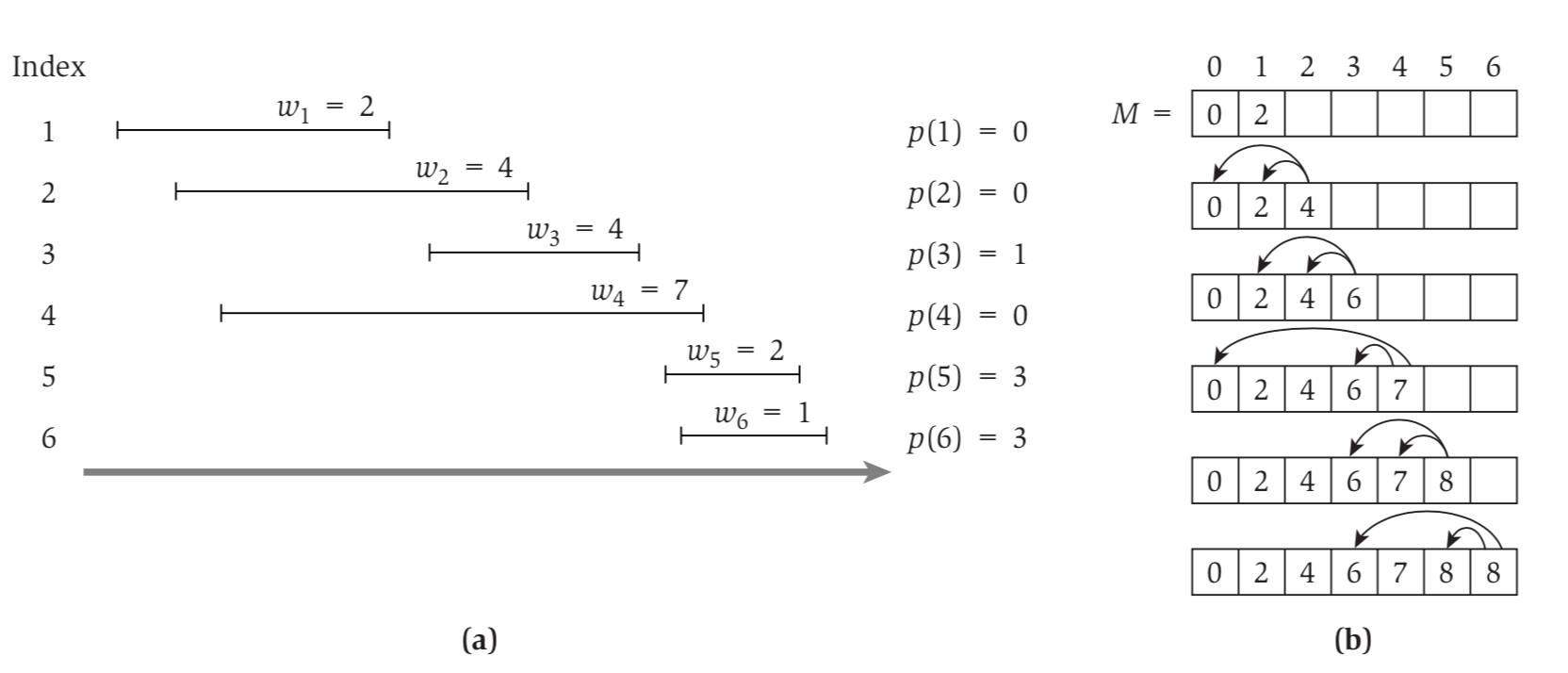
Analysis

In M-Compute-Opt M has at most n + 1 entries, the run time is O(n).

Find-solution will exceute at most n recursive call, so O(n).