Segmented Least Square

Problem¹

Data $P = (x_1,y_1), (x_2, y_2)…(x_n, y_n)$ for $x_1 < x_2 < … < x_n$.

Given a line y=ax+b, and error

$$Error(L, P) = \sum_{i=1}^n(y_i - ax_i -b)^2$$

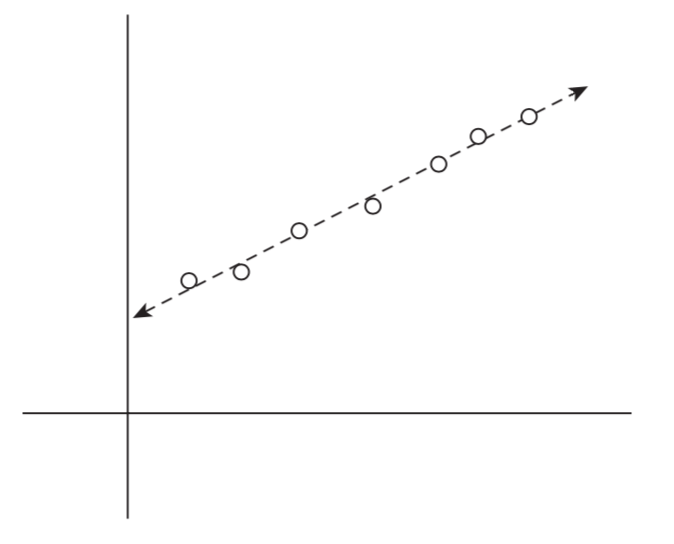
And it has closed form solution of

$$a = \frac{n\sum_i x_iy_i - (\sum_i x_i)(\sum_i y_i)}{n\sum_i x_i^2 - (\sum_i x_i)^2}$$

and

$$b = \frac {\sum_i y_i - a \sum_i x_i}{n}$$

However, if the data is show as below (maybe fitted with two lines), we can’t just use the above formula.

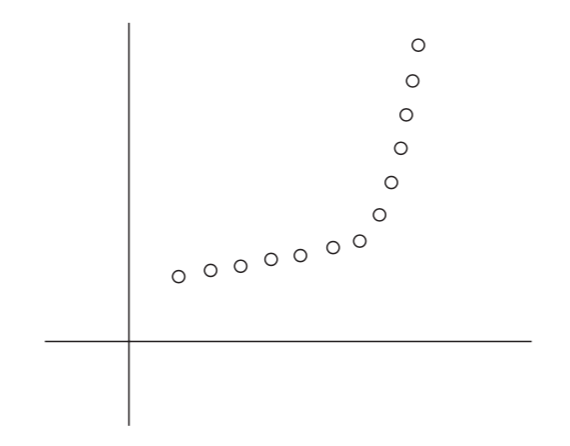
Formulated Problem

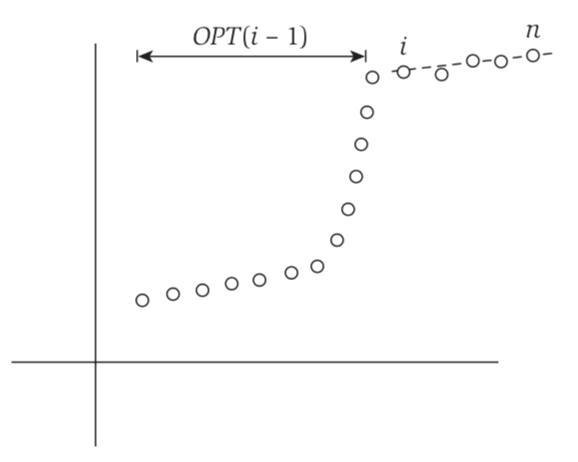
• $P = {p_i | i = 1\ to\ n}$, where $p_i = (x_1, y_1)$, with x1 < x2 < … < xn
• observing that $p_n$ belongs to a segment, and that segment start at some index i
• then we can recursively look for $p_1 …, p_{i-1}$.
• OPT(i) = Optimal solution for $p_i, …, p_i$.
• $OPT(n) = e_{i,n} + C + OPT(i − 1)$
• $OPT(j) = \min_{1≤i≤j} (e_{i,j} + C + OPT(i − 1))$ (6.7)

Algorithm

Segmented-Least-Squares(n)

• Array M[0…n]
• Set M[0]=0
• For all pairs i≤j
  • Compute the least squares error $e_{i , j}$ for the segment $p_i , … , p_j$
• EndFor
• For j=1,2,…,n
  • Use the recurrence (6.7) to compute M[j]
• Endfor
• Return M[n]

Analysis

Perform error, $e_{i,j}$, calculation for all pair of i and j takes O($n^2$) to loop and O(n) based on formula, so overall O($n^3$) times.

To get OPT takes O($n^2$).