RNA Secondary Structure

Problem¹

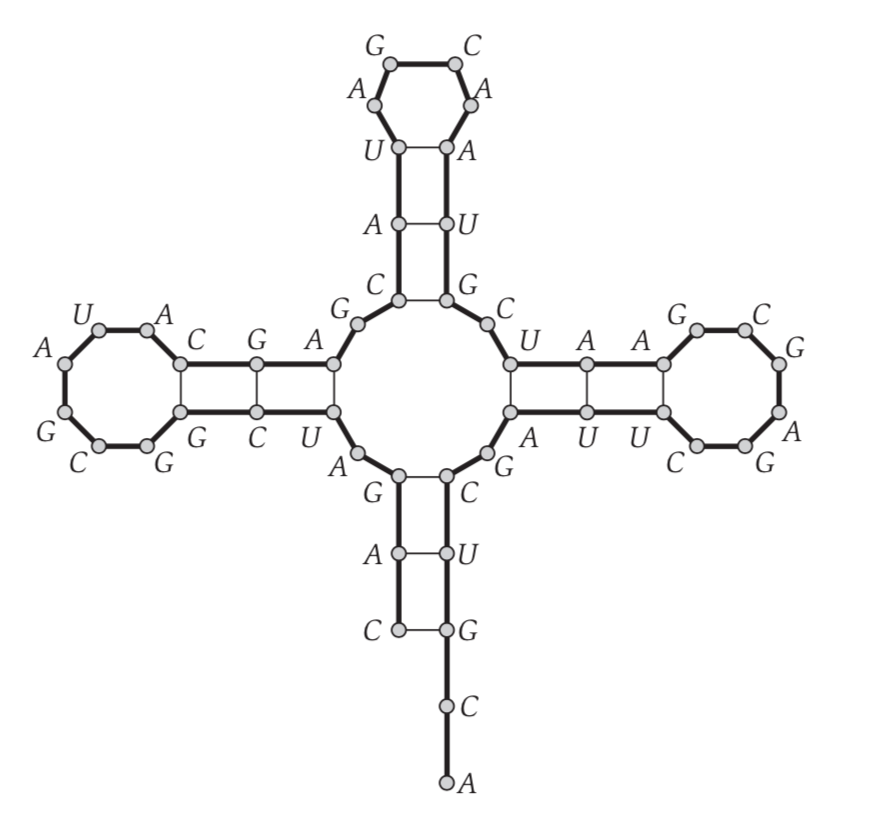
We have bases of {A,C,G,T} in DNA sequence, where A-T and C-G form a pair. A sinlge strand of RNA will loop back, resulting shape called secondary structure.

Let $B = b_1b_2 … b_n$, where $b_i$ = {A,C,G,U} also A-U, C-G form pair

Then the Secondary structure, S ={(i, j)}

• no sharp turn, i < j - 4
• pair is either {A,U}, {C,G} (either order)
• no base appear in more than 1 matching
• no crossing condition, (i,j) and (k, l) $\in$ S, we can’t have i < k < j < l

Algorithm

Following the same analysis

• OPT(j) = the maximum number of base pairs in a secondary structure on $b_1b_2 … b_j$.
• OPT(j) = 0 for j $\leq$ 5

The above rules (constraints) make the recurrent relationship

• j is not involved in a pair
• j pairs with t for some t < j − 4

Then we split the problem into two cases due to noncrosing constriant (no pair form between first part and second part)

• from 1 to t - 1 using OPT(t − 1)
• from t + 1 to j - 1 which is not considered by our OPT

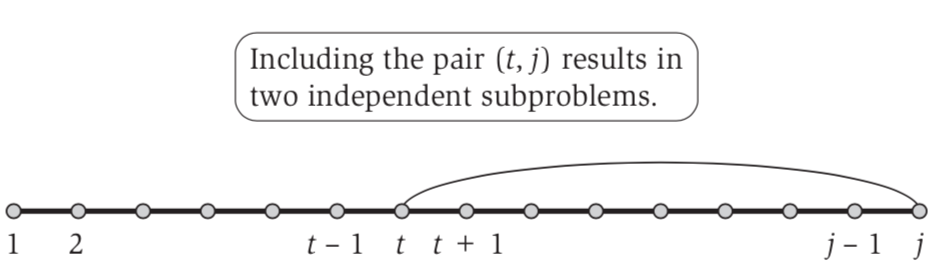
This push our OPT take take another paramter i, so OPT(i,j) = maximum number of base pairs in a secondary structure on $b_ib_{i+1} … b_j$.

Therefore, OPT(i, j) = max(OPT(i, j − 1), max(1 + OPT(i, t − 1) + OPT(t + 1, j − 1))) （6.13).

• Initialize OPT(i,j)=0 whenever i≥j−4
• For k=5, 6,…,n−1
  • For i=1,2,…n−k
    • Set j=i+k
    • Compute OPT(i, j) using the recurrence in (6.13)
  • Endfor
• Endfor Return OPT(1, n)

Analysis

There are $O(n^2)$ subproblems to solve, and evaluating the recurrence in (6.13) takes time O(n) for each. So overall $O(n^3)$.