Network Flow

Problem¹

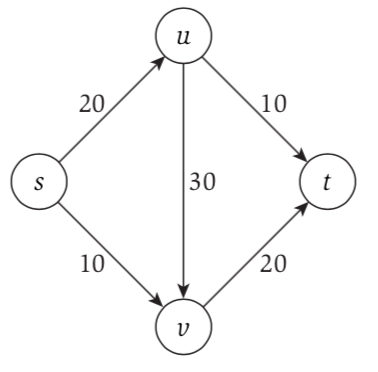
A G(V, E), with each edge is capacity $C_e$.

The is source s $\in$ and sink t $\in$ V.

No edge enter and and no edge leaving t.

Flow is defined as function f that take the edge and return a nonnegative real number, $f: E \rightarrow R^+$

Subjects to following constraints

1. $0 \leq f(e) \leq c_e$
2. $\sum_{e\ into\ v} f(e) = \sum_{e\ out\ of v} f(e)$ or $f^{out}(v) = f^{in}(v)$

GOAL: find the maximum flow.

Algorithm

Residual Graph

Comes from the idea of following

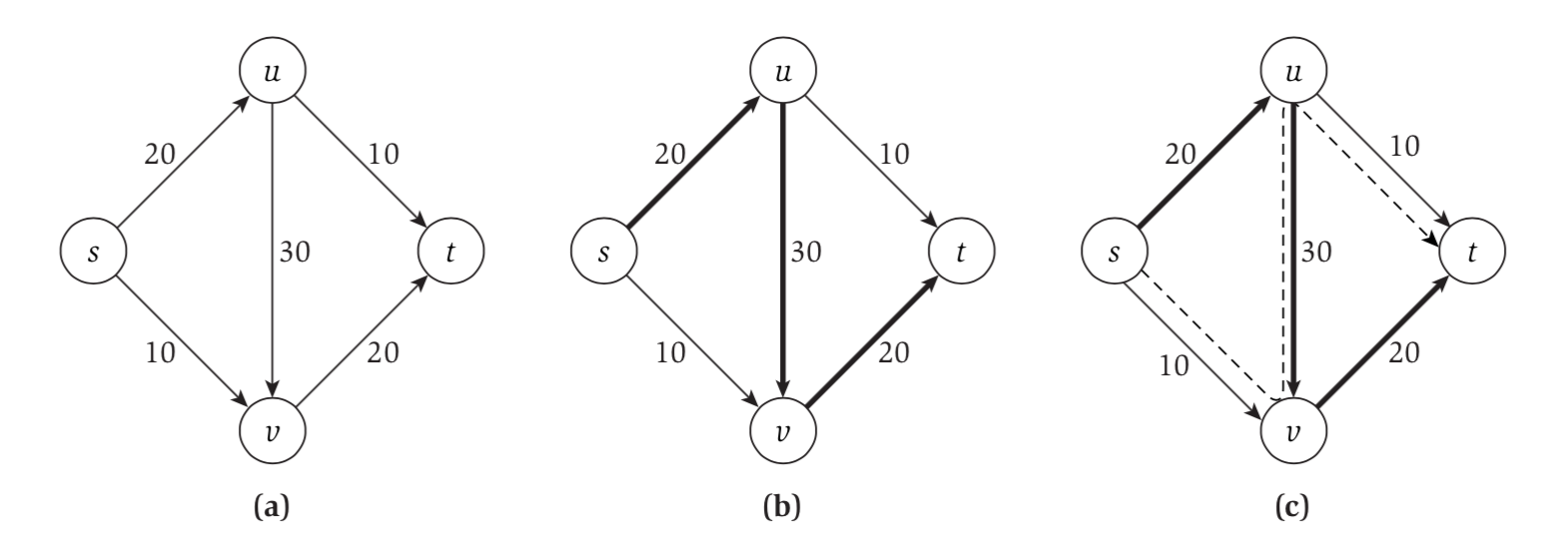
At first, we can push 20 units from S -> u -> v -> t. However, one can clearly see that the maximum is 30. But we are stuck now, because any additional flow will exceed the capacity of the edge. When we push s->v with the flow of 10, we need to undo 10 units on the u->v edge.

Residual graph $G_f$ is defined as follow:

• same node set as G
• for each edge e = (u,v) of G which f(e) < $c_e$, there is $c_e - f(e)$ leftover forward flow
• there is also f(e) is backward flow which we can undo

Augmenting Path

augment(f , P)

1. Let b=bottleneck(P,f)
2. For each edge (u,v) $\in$ P
   • If e=(u,v) is a forward edge then
     • increase f(e) in G by b
   • Else ((u, v) is a backward edge, and let e = (v, u))
     • decrease f(e) in G by b
   • Endif Endfor
3. Return(f)

Claim f’ = augment(f,P) is a flow in g

If f is forward flow, the conditions holds, because of following $$0 \leq f(e) \leq f′(e) = f(e) + bottleneck(P, f) \leq f(e) + (c_e − f(e)) = c_e$$

If f is backward flow, the conditions holds, because of following $$c_e \geq f(e) \geq f′(e) = f(e) − bottleneck(P, f) \geq f(e) − f(e) = 0$$

The conversation of mass is also holds.

Ford-Fulkerson Algorithm Max-Flow

1. Initially f(e) = 0 for all e in G
2. While there is an s-t path in the residual graph $G_f$
   • Let P be a simple s-t path in $G_f$
   • f’ = augment(f, P)
   • Update f to be f’
   • Update the residual graph Gf to be Gf′
3. Endwhile
4. Return f

Analysis

Assume all residuals are all integers, and the algorithm will terminate

v(f’) = v(f) + bottleneck(P, f), since bottleneck(P, f) > 0, then v(f’)>(f).

The first edge e leaving s must be a forward flow, so we increase the flow by bottleneck(P,f). Moreover, we maximum number of iteration we can have is $\sum_{e\ out\ of\ s} c_e$ if we increase flow by 1 unit at the time.

Time Complexity

The algorithm takes O(m + n), where n = number of nodes, m = number of edges. Since m $\geq$ n/2, we can simplify to O(m). Combined with the max capacity at the s, we have O(mC). Finding path takes O(m+n) = O(m), augmenting takes O(n), building residual graph takes O(m). Overall, it takes $O(m^2C)$.

Cut

Divide the graph into two set, A contains s and B contains t. The capacity of this cut c(A,B)= $\sum_{e\ out\ of\ A}c_e$.

Claim

However, we can provide an even strong upper bound, $v(f) = f^{out}(A) − f^{in}(A)$.

Proof

• By definition $v(f) = f^{out}(s)$
• Since $f^{in}(s) = 0$, we can writer above as $v(f) = f^{out}(s) - f^{in}(s)$
• $v(f) = \sum_{v \in A}(f^{out}(v) − f^{in}(v))$, where all node != s will contribute 0 to the sum
• RHS = $\sum_{e\ out\ of\ A} f(e) - \sum_{e\ into\ A} f(e) = f^{out}(A) - f^{in}(A)$
• Base case, A = {s}, then $f^{out}(A) = f^{out}(s)$, $f^{in}(A) = 0$
• If (A, B) is a cut, $f^{out}(A) = f^{in}(B)$ and $f^{in}(A) = f^{out}(B)$, so $ v(f) = f^{in}(B) - f^{out}(B)$
• The above also proof the base case of B = {t}

Claim

$$v(f ) \leq c(A, B)$$

Proof

\begin{align} v(f) &= f^{out}(A) - f^{in}(A) \newline &\leq f^{out}(A) \newline &= \sum_{e\ out\ of\ A} f(e) \newline &\leq \sum_{e\ out\ of\ A} c_e \newline &= c(A,B) \end{align}

Basically, we are saying that the flow is upper bounded by its capacity of cut.

Max Flow = Min Cut

Claim

$v(\bar{f}) = c(A^*, B^*)$, where $\bar{f}$ = flow return by Ford-Fulkerson Algorithm.

Proof

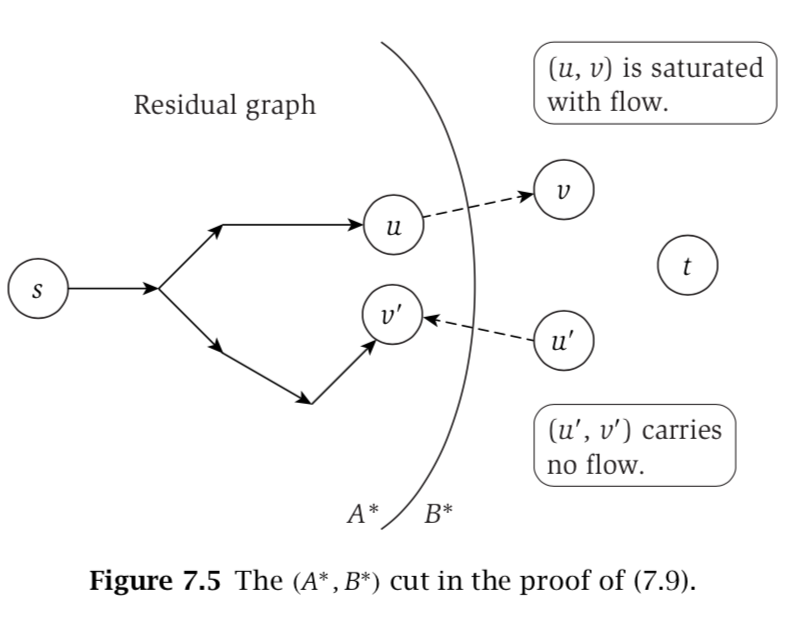
1. $(A^*, B^*)$ is a cut
   • $s \in A$ and $t \in B$
2. e=(u,v) and $f(e) = c_e$
   • if not, there is path from s to v path in $G_f$ which contradicts $v \in B^*$
3. similiary e’=(u’,v’) and $f(e’) = 0$

So \begin{align} v(f) &= f^{out}(A^*) - f^{in}(A^*) \newline &= \sum_{e\ out\ of\ A} f(e) - \sum_{e\ into\ A} f(e)\newline &= \sum_{e\ out\ of\ A} c_e - 0\newline &= c(A^*, B^*)\newline \end{align}

More generally in every cut, v(f)=c(A,B).

Therefore, if there is f’ > f, this will f’ will exceed the capacity now if there is c(A’,B’) < $c(A^*, B^*)$, it will be < v(f), both of them contradict v(f) ≤ c(A, B).