Merge Sort
Problem
Sort the elements
Abstract the behavior:
1. Divide the input into two pieces of equal size O(n)
1. solve the two subproblems on these pieces separately by recursion
1. combine the two results into an overall solution O(n)
Recurrence
Time Complexity
q = 2
T(n) ≤ 2T(n/2) + cn
To analyze the above recurrence relation, check below image.
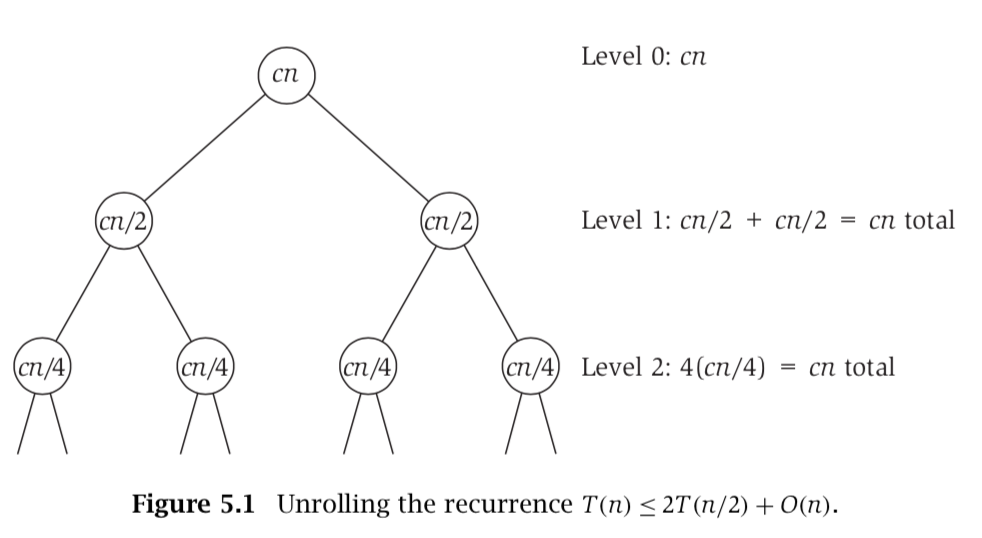
- At level j, we have $2^j$ nodes with size $n/2^j$
- Each node takes $cn/2^j$, so level j takes $cn/2^j$ x $2^j = cn$
- There are logn levels, so T(n) = O(nlogn)
General Case
For q > 2
T(n) ≤ qT(n/2) + cn
Solving directly
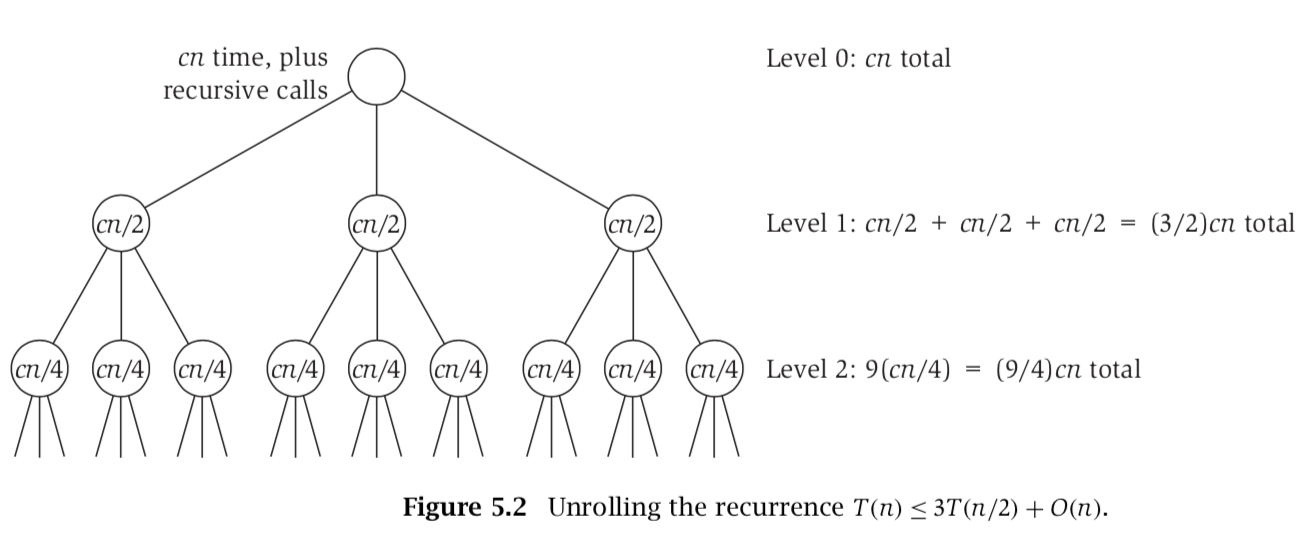
- At level j, we have $q^j$ nodes with size $n/2^j$
- Each node takes $cn/2^j$, so level j takes $cn/2^j$ x $q^j = (q/2)^jcn$
- So $$T(n) \leq cn\sum_{j=0}^{\log_2 {n-1}}(\frac{q}{2})^j$$
Since this is a geometric series with r = q/2 $$T(n) \leq cn\frac{r^{\log_2 n} - 1}{r - 1} \leq cn\frac{r^{\log_2 n}}{r - 1}$$
We then move the r - 1 out to form the constant $$T(n) \leq \frac{c}{r - 1}nr^{\log_2 n}$$
To figure out what is $r^{\log_2 n}$, we use $a^{\log b} = b^{\log a}$ when a > 1 and b > 1.
So, $r^{log_2 n} = n^{\log_2 r} = n^{\log_2 \frac{q}{2}} = n^{{\log_2 q} - 1}$
Thus, we have $$T(n) \leq \frac{c}{r - 1}nn^{\log_2 q - 1} \leq \frac{c}{r - 1}n^{\log_2 q} = O(n^{\log_2 q})$$
Alternative
We guess $$T(n) \leq kn^d$$ which leads to \begin{align} T(n) &\leq qT(n/2) + cn \newline & = qk(n/2)^d +cn \newline & = \frac{q}{2^d}kn^d + cn \end{align} Choosing $2^d = q$ -> $d = \log_2 q$ $$T(n) \leq kn^{\log_2 q} + cn$$ However, there is cn left. We guess another solution. $$T(n) \leq kn^d - ln$$ which leads to \begin{align} T(n) &\leq qk(n/2)^d - ql(n/2)+cn \newline & = \frac{q}{2^d}kn^d - \frac{ql}{2}n+cn \newline & = kn^d - \frac{ql}{2}n+cn \newline & = kn^d - (\frac{ql}{2} - c)n \end{align}
For q = 1
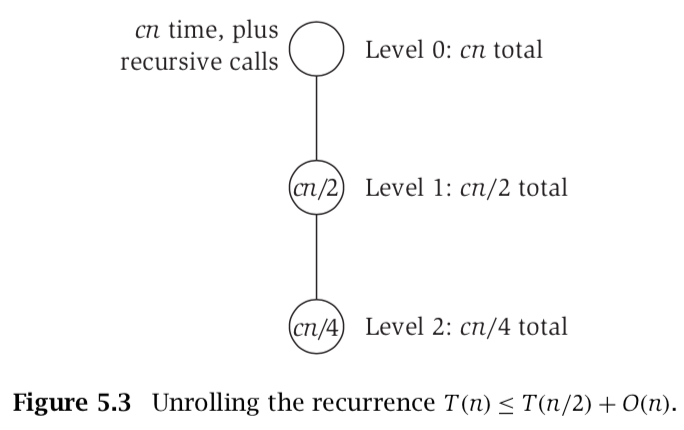
- At first level we have $O(cn)$, next level we have $O(cn/2)$
- At level j, we have work of $O(cn/2^j)$
- So total amount of work \begin{align} T(n) &\leq cn\sum_{j=0}^{\log_2 {n-1}} \frac{1}{2^j} \newline &= 2cn \newline &= O(n) \end{align}
Another Look at Mergesort
if divide and combine takes $O(n^2)$ The recurrence relation becomes $$T(n) \leq 2T(n/2) + cn^2$$
- First level, size n, takes $cn^2$. In next level, it takes $c(n/2)^2 = c{n^2}/4$, total of $c{n^2}/2$. Third level, total of $c{n^2}/4$.
- for level j, then we have $c{n^2}/2^j$
- So $$T(n) \leq cn^2 \sum_{j=0}^{\log_2 {n - 1}} (\frac{1}{2^j}) \leq 2cn^2 = O(n^2)$$