Logistic Regression

Uncertainty in Prediction

Related to Linear Regression.

The available features x do not contain enough information to perfectly predict y, such as

• x = medical record for patients at risk for a disease
• y = will he contact disease in next 5 years

Model

We still going to use linear model for conditional probability estmation

$$w_1x_1 + w_2x_2 + … + w_dx_d + b = w \cdot x + b$$

We want the Pr(y=1):

• increases as linear function grows
• 0.5 when linear function is 0

This leads to the sigmoid function

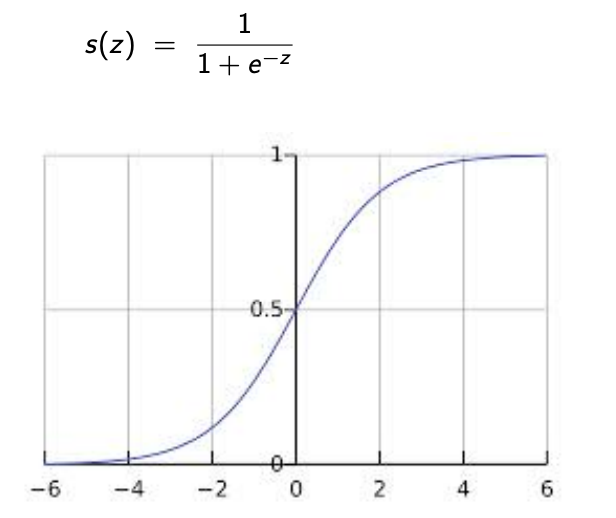
Logistic Regression Model

Let $y \in$ {-1, 1}

$$Pr(y = 1 | x) = \frac{1}{1 + e^{-(w \cdot x + b)}}$$

and

$$Pr(y = -1 | x) = 1 - Pr(y = 1 | x) = \frac{1}{1 + e^{w \cdot x + b}}$$

Or consisely

$$Pr(y | x) = \frac{1}{1 + e^{-y(w \cdot x + b)}}$$

Maximum-likelihood

We want to maximize the probability:

$$\prod_{i=1}^n Pr_{w,b}(y^{(i)}|x^{(i)})$$

Loss function

After taking log of maximum-likelihood formula, we convert it to the loss function

$$L(w, b) = - \sum_{i=1}^n \ln Pr_{w,b}(y^{(i)}|x^{(i)}) = \sum_{i=1}^n \ln (1 + e^{-y^{(i)}(w \cdot x^{(i)} + b)})$$

Solution

There is no closed-form solution for w, but L(x) is convex.

Convexity is crucial because the local minimum is also the global minimum.

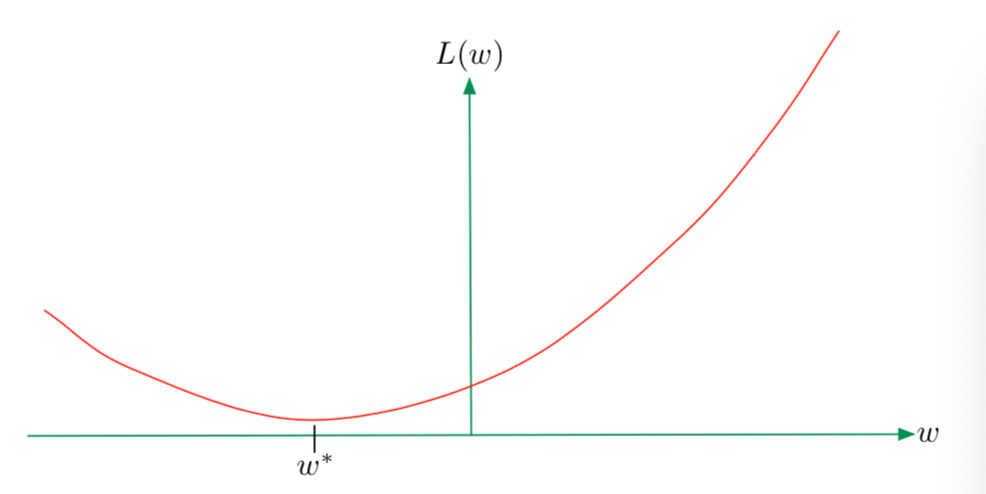
We turn to numerical method gradient descent.

Gradient Descent

1. Set $w_0 = 0$
2. For t = 0, 1, 2, … until convergence:
   • $w_{t+1} = w_t + \eta_t \sum_{i=1}^n y^{(i)}x^{(i)}Pr_{w_t}(-y^{(i)} | x^{(i)})$, where $\eta_t$ is called step size (learning rate)