Linear Regression
Basic Idea
Fit a line to a bunch of points.
Example
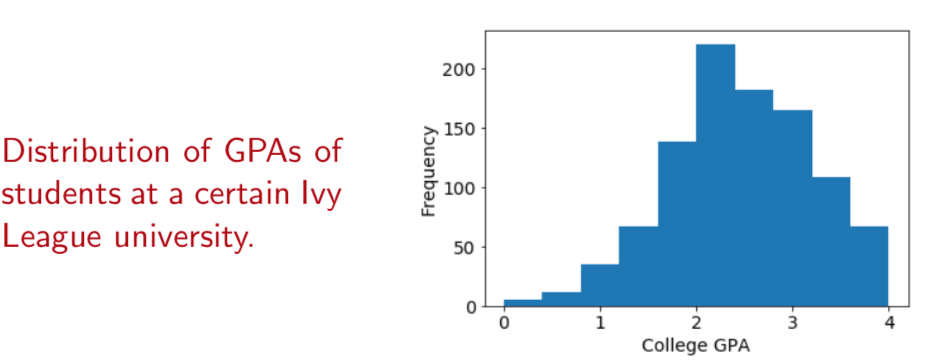
Without extra information, we will predict the mean 2.47.
Average squared error = $\mathbb{E} [(studentGPA - predictedGPA)^2]$ = Variance
If we have SAT scores, then we can fit a line.
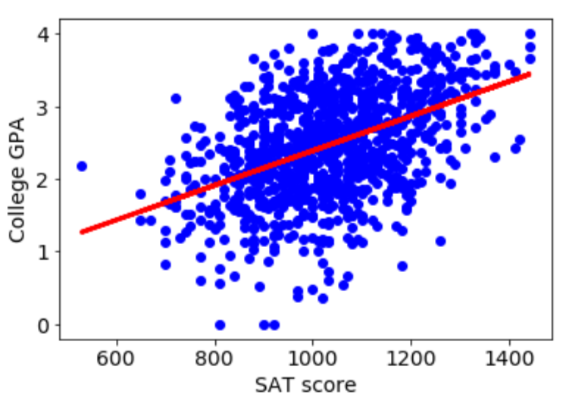
Now if we predict based on this line, the MSE drops to 0.43.
This is a regression problem with:
- Predictor variable: SAT score
- Response variable: College GPA
Formula
For $\mathbb{R}$ $$y = ax + b$$
For $\mathbb{R}^10$ $$f(x) = w_1x_1 + w_2x_2 + … + w_{10}x_{10} + b = wx + b$$
where $w = (w_1, w_2, …, w_{10})$
Loss Function
MSE is follow $$MSE(a, b) = \frac{1}{n} \sum_{i=1}^n (y^{(i)} -(ax^{(i)} + b))^2$$
and loss function for $\mathbb{R}$ $$L(a, b) = \sum_{i=1}^n (y^{(i)} -(ax^{(i)} + b))^2$$
Analagously for $\mathbb{R}^d$
$$L(w, b) = \sum_{i=1}^n (y^{(i)} -(w \cdot x^{(i)} + b))^2$$ where $x \in \mathbb{E}^d$, $y \in \mathbb{E}$, $w \in \mathbb{E}^d$, and $b \in \mathbb{E}$
Alternatively, we can write as: $$f(x) = \tilde{w} \cdot \tilde{x}$$ $$L( \tilde{w} ) = \sum_{i=1}^n (y^{(i)} - \tilde{w} \cdot \tilde{x}^{(i)})^2$$ where $\tilde{x} = (1, x) \in \mathbb{E}^{d+1}$ and $\tilde{w} = (b, w) \in \mathbb{E}^{d+1}$, and minimized at $\tilde{w} = (X^TX)^{-1}(X^Ty)$
Regularization
Regularization term is crucial in avoiding complex model. This term is introduced as follow:
$$L(w, b) = \sum_{i=1}^n (y^{(i)} -(w \cdot x^{(i)} + b))^2 + \lambda||w||^2$$ and the solution is $w = (X^TX + \lambda I)^{-1}(X^Ty)$
With the help of regularizer, we avoid the complex molde (overfitting the data), and obtain a better performance on test set.
| λ | training MSE | test MSE |
|---|---|---|
| 0.00001 | 0 | 585.81 |
| 0.0001 | 0 | 564.28 |
| 0.001 | 0 | 404.08 |
| 0.01 | 0.01 | 83.48 |
| 0.1 | 0.03 | 19.26 |
| 1 | 0.07 | 7.02 |
| 10 | 0.35 | 2.84 |
| 100 | 2.4 | 5.79 |
| 1000 | 8.19 | 10.97 |
| 10000 | 10.83 | 12.63 |
Ridge Regression
$$L(w, b) = \sum_{i=1}^n (y^{(i)} -(w \cdot x^{(i)} + b))^2 + \lambda||w||_2^2$$
Lasso Regression (Produce sparse w)
$$L(w, b) = \sum_{i=1}^n (y^{(i)} -(w \cdot x^{(i)} + b))^2 + \lambda||w||_1$$
Key differene1:
- Ridge works well for overfitting
- Lasso shrinks less important features, good for feature selection
- L1 and L2 Regularization Methods, https://towardsdatascience.com/l1-and-l2-regularization-methods-ce25e7fc831c [return]