Knapsack

Problem¹

Each request has value $v_i$ and weight $w_i$, and we have constraint that the total of request weight $\leq$ W.

Greedy doesn’t work because sorting the W either in decreasing or increasing manner don’t produce the optimal solution.

• {W/2 + 1, W/2, W/2}
• {1, W/2, W/2}

Using dynamic programing, we can use reduce this problem to whether or not each request belongs to the optimal solution O again.

• If $n \notin O$, $OPT(n, W) = OPT(n − 1, W)$
• If $n \in O$, $OPT(n,W)=w_n+OPT(n−1,W−w_n)$

Overall, we have following rule

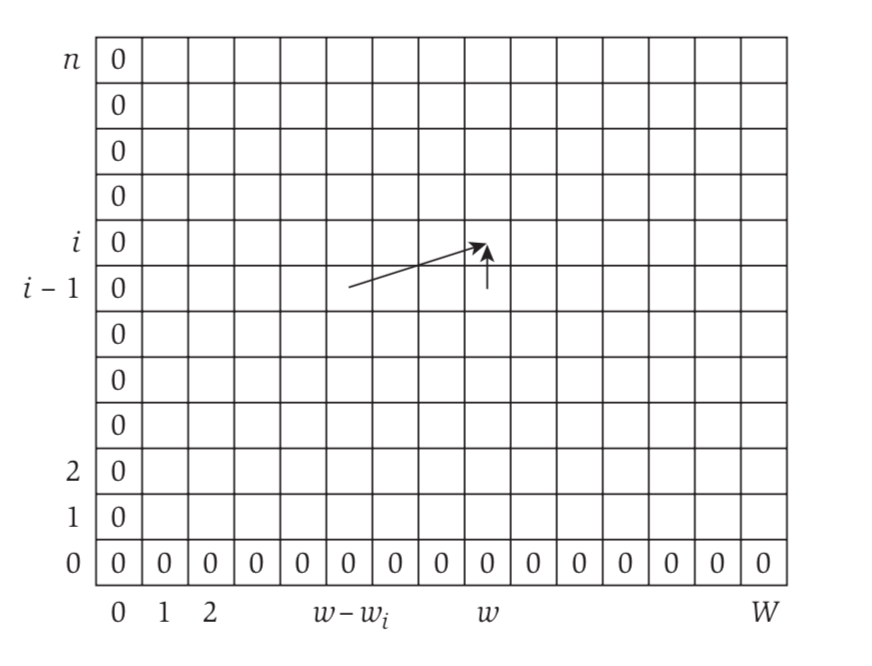
• If $w < w_i$ then OPT(i, w) = OPT(i − 1, w)
• Otherwise OPT(i,w)=$\max$(OPT(i−1,w),$w_i$ +OPT(i−1,w−$w_i$))

Algorithm

Subset-Sum(n, W)

• Array M[0…n,0…W]
• Initialize M[0,w]=0 for each w=0,1,…,W
• For i=1,2,…,n
  • For w=0,…,W
    • Use the recurrence (6.8) to compute M[i, w]
  • Endfor
• Endfor
• Return M[n, W]

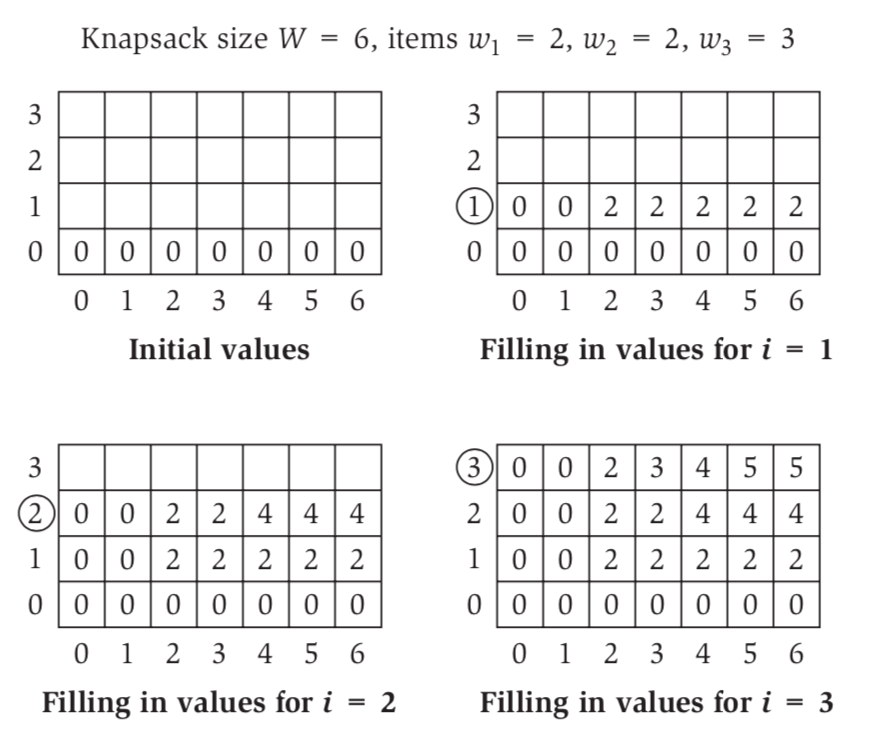
Example

Analysis

Clearly O(nW), so called pseudo-polynomial.

If we extend the problem to include the value, we can simply switch to following:

• If $w < w_i$ then OPT(i, w) = OPT(i − 1, w)
• Otherwise OPT(i,w)=$\max$(OPT(i−1,w),$v_i$ +OPT(i−1,w−$w_i$)).