K Clustering
Problem
We have set of objects $U = \{o_1, o_2, …\}$, and we want to split them into k clusters.
We also have following definition for distance function.
- $\forall_{i,j} dist(p_i, p_j) = dist(p_j, p_j)$
- $\forall_{i,j} dist(p_i, p_i) = 0$
- $\forall_{i,j} dist(p_i, p_j) > 0$.
At the end, we should have $C = \{C_1, C_2, … C_K\}$.
Let’s define spacing to be the minimum dist between clusters. Our goal is to find the k-clustering with maximum spacing.
Algorithm
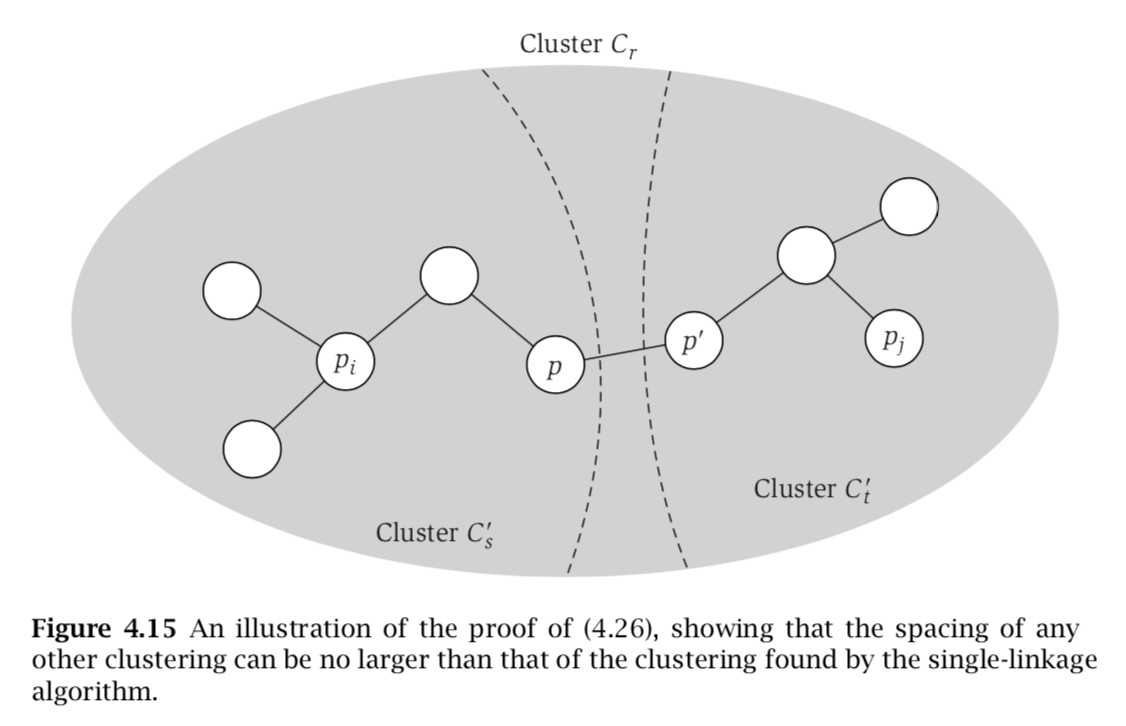
Kruskal’s Algorithm
- Sort the edges using dist as edge weight
- In each iteration, pick the min edge that doesn’t form cycle
- The connected component = cluster
- Connecting (merge) two clusters with new edge = single-link clustering
- Stops when we have k components
- equivalent of stop before adding last k - 1 edges for Kruskal’s Algorithm
Below is picture of single-linked clusters with k = 3.
Analyzing Algorithm
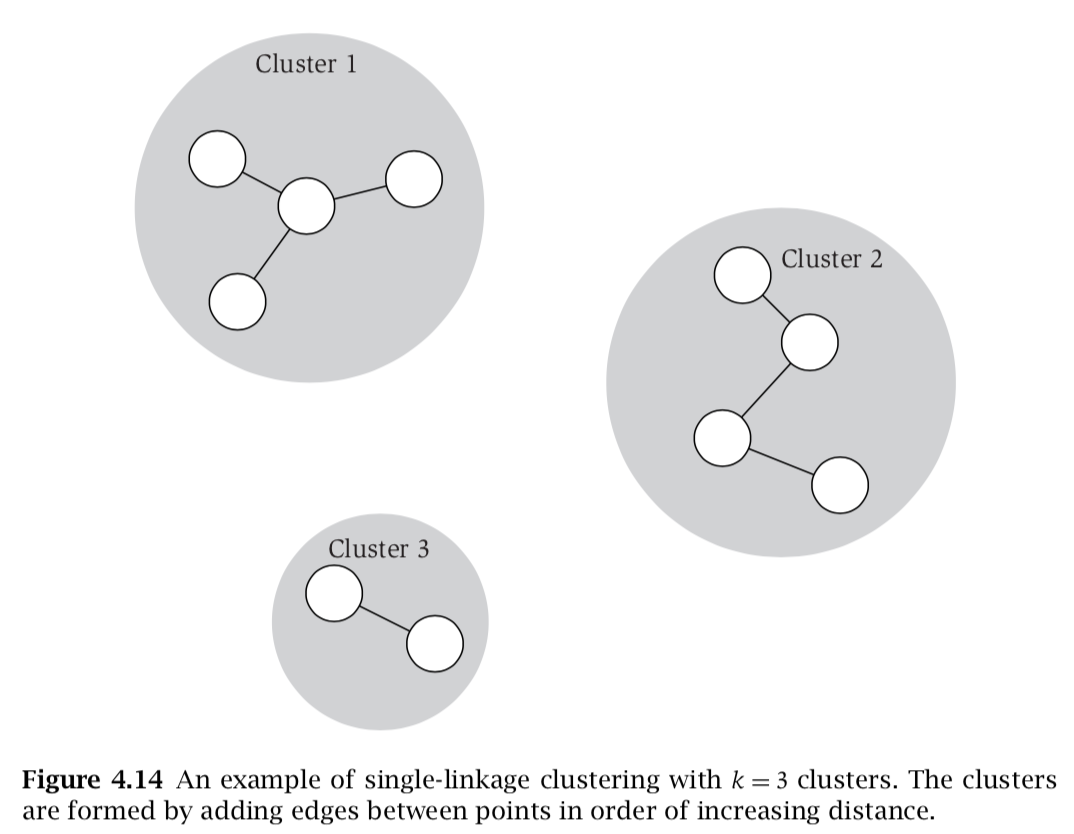
Claim: The components $C_1, C_2, …, C_k$ formed by deleting the k − 1 most expensive edges of the minimum spanning tree T constitute a k-clustering of maximum spacing.
Proof:
- $\mathbb{C} = \{C_1, C_2, …, C_k\}$
- $d^{*} = (k - 1)$ most expensive edge (since algorithm stops here)
- Assume there is $\mathbb{C’} = \{C’_1, C’_2, …, C’_k\}$
- $\exists C_r$ that contains $p_i$ and $p_j$
- S.T. $C_r \subsetneq C’_s$ and $C_r\subsetneq C’_t$
- $p_i \in C’_s$, $p_j \in C’_t$ and $s \neq t$
- Since $p_i$ and $p_j \in C_r$, there is path between them
- On Kruskal’s algorithm, all these edges in the path are at most d*
- Assume $p \in C’s$ and $p’ \in C’t$ that were connected before
- p - p’ was one of the edges, $d(p, p’) \leq d*$
- Spacing $\mathbb{C’} \leq d*$