Integer Multiplication
Problem

Algorithm
Let’s say we define $x = x_1 2^{n/2} + x_0$, then xy become \begin{align} xy &= (x_1 2^{n/2} + x_0)(y_1 2^{n/2} + y_0) \newline &= x_1 y_1 2^n + (x_1 y_0 + x_0 y_1)2^{n/2} + x_0 y_0 \end{align}
So we have $$T(n) \leq 4T(n/2) + cn$$ But this is essentially $$T(n) \leq O(n^{\log_2 q}) = O(n^2)$$
However, we can reduce the time by observing that $(x_1 + x_0)(y_1 + y_0) = x_1y_1 + x_1y_0 + x_0y_1 + x_0y_0$. The outermost terms are $x_1y_1$ and $x_0y_0$, the middle terms = $(x_1 + x_0)(y_1 + y_0) - x_1y_1- x_0y_0$.
The Algorithm
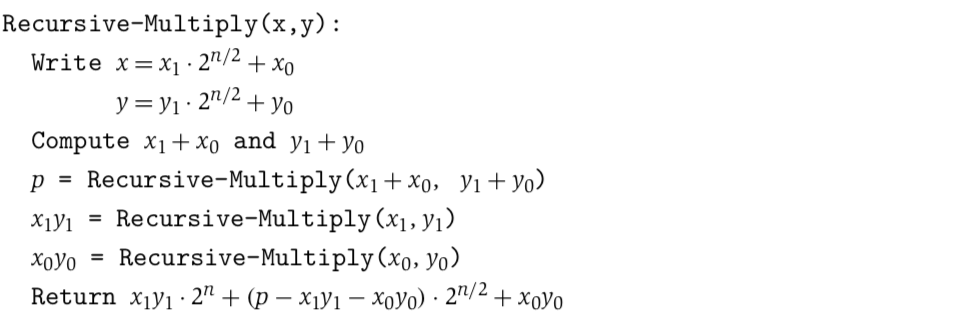
So we have $$T(n) \leq 3T(n/2) + cn = O(n^{\log_2 3}) = O(n^{1.59})$$