Gradient Descent
Gradient Descent
A simple algorithm to go “downward” against the gradient of the function.
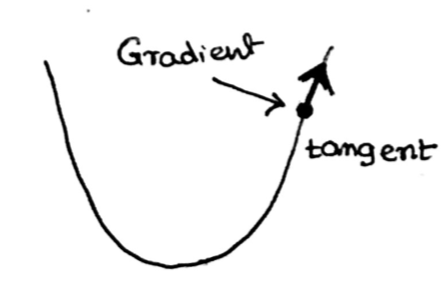
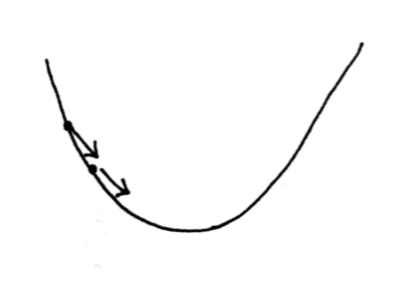
Algebrically: $$w_{t+1} = w_t - \eta \nabla f(w_t)$$ where $\eta$ is called learning rate or step size.
Step Size
- $\eta$ too small, slow convergence
- $\eta$ too large, solution will bounce around
In practice:
- Set $\eta$ to be a smalle constant
- Backtracking line search (work when $\nabla f$ is continuous)
- Parameter $\bar{\alpha}, c \in (0,1), \rho \in (0,1)$. Descent direction $P_t$ (an negative value input to the algorithm, could be against gradient but doesn’t have to).
- Set $\alpha = \bar{\alpha}$
- Rpeat until $f(x_t + \alpha P_t) \leq f(x_t) + c \alpha \nabla f(x_t)^T P_t$
- $\alpha \gets \rho\alpha$
- Terminate with $\eta_t = \alpha$