Fast Fourtier Transform
Problem
Given two vectors $a = (a_1, a_2, a_{n-1})$ and $b = (a_1, b_2, b_{n-1})$.
The convolution of a * b is a vector with 2n - 1 coordinates, where coordinate k is $\sum_{(i,j):i+j=k|i,j < n} a_ib_j$, which is can be written as
$$a ∗ b = (a_0b_0, a_0b_1 + a_1b_0, a_0b_2 + a_1b_1 + a_2b_0, … , a_{n−2}b_{n−1} + a_{n−1}b_{n−2}, a_{n−1}b_{n−1})$$
Or an n x n table, whose (i, j) entry is $a_ib_j$
\begin{bmatrix} a_0b_0 & a_0b_1 & … & a_0b_{n-2} & a_0b_{n-1}\newline a_1b_0 & a_1b_1 & … & a_2b_{n-2} & a_1b_{n-1}\newline a_2b_0 & a_2b_1 & … & a_2b_{n-2} & a_2b_{n-1}\newline … & … & … & … & … \newline a_{n-1}b_0 & a_{n-1}b_1 & … & a_{n-1}b_{n-2} & a_{n-1}b_{n-1} \end{bmatrix}
Then the convolution is suming along the diagonols. The motivation for convultion lies on the polynomial applications, signaling.
Extra notes
For example, we have a vector representing the measurement. We would like to smooth out the noise for each measurement $a_i$ with weighted sum of its left neighbors and right neighbors within k steps.
Algorithm
Preprocess:
- Choose 2n values $x_1, x_2, …, x_{2n}$, evaluate $A(x_j)$ and $B(x_j)$ for j=1 … 2n
- $C(x_j) = A(x_j)B(x_j)$
- Reconstruct $C(x_j)$ from its values on $x_1, x_2, …, x_{2n}$
The Complex Roots of Unity
Complex Number
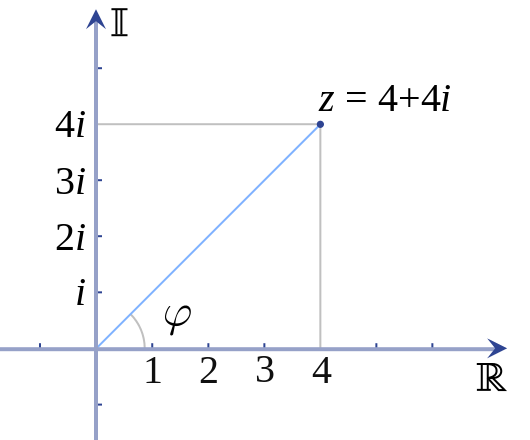 A complex number can be represented in rectangular form as $z = x + iy$.
A complex number can be represented in rectangular form as $z = x + iy$.
Or $z = r(cos\theta + isin\theta)$
Or in polar coordinate $z = re^{\theta i}$
Combine these, we get $e^{i\theta} = cos\theta + sin\theta$ Plug in $\theta = \pi$, we got $e^{i\pi} = -1$, which leads to the Euler’s identity $e^{i\pi} + 1 = 0$.
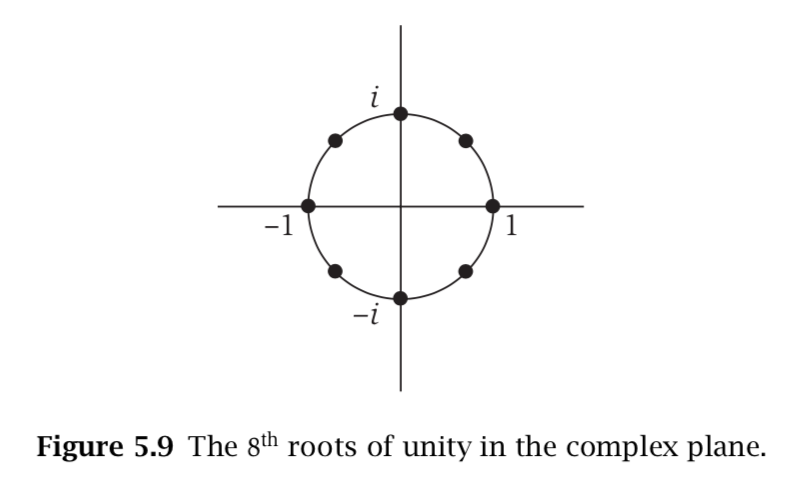
For each polynomial equation $x^k = 1$, the complex roots $\omega_{j,k} = e^{2\pi ji/k}$, since $(e^{2\pi ji/k})^k = e^{2\pi ji} = (e^{2\pi i})^j = 1 ^ j = 1$. We refer $\omega$ as the kth root of unity.
For k = 8, we got following
Step 1.
Going back to the evaluating A(x), let’s split A(x) into
$$A_{even}(x) = a_0 + a_2x + a_4x^2 + … + a_{n−2}x^{(n−2)/2}$$
and
$$A_{odd}(x) = a_1 + a_3x + a_5x^2 + … + a_{n−1}x^{(n−2)/2}$$
And $A(x) = A_{even}(x^2) + xA_{odd}(x^2)$
Step 2. Now considering we got the 2nth root of unity, $\omega_{j,2n} = e^{2\pi ji/2n}$, we can simply obtain the nth root by squaring the 2nth root, $\omega_{j,k}^2 = e^{2\pi ji/n}$. This only takes constant operation, so we got $$A(\omega_{j, 2n}) = A_{even}(\omega_{j, 2n}^2) + \omega_{j, 2n}A_{odd}(\omega_{j, 2n}^2)$$
Step 3. For $C(\omega_{j,n}) = A(\omega_{j,2n})B(\omega_{j,2n})$, it takes O(n) times. Reconstruction takes similar approach as before. Let’s define C(x) $C(x) = \sum_{s=0}^{2n-1} c_sx^s$, which we want to reconstruct from its values $C(\omega_{s,2n})$ at 2nth root of unity. Let’s define another $D(x) = \sum_{s=0}^{2n-1} d_sx^s$ where $d_s = C(\omega_{s,2n})$. Then,
\begin{align} D(\omega_{j,2n}) &= \sum_{s=0}^{2n - 1}C(\omega_{s,2n})\omega_{j,2n}^s \newline &= \sum_{s=0}^{2n - 1} (\sum_{t=0}^{2n - 1} c_t\omega_{s,2n}^t)\omega_{j,2n}^s \newline &= \sum_{t=0}^{2n - 1} c_t(\sum_{s=0}^{2n - 1} \omega_{s,2n}^t\omega_{j,2n}^s) \end{align}
Using the fact that $\omega_{s,2n} = (e^{2pii/2n})^s$, the above expression \begin{align} D(\omega_{j,2n}) &= \sum_{t=0}^{2n - 1} c_t(\sum_{s=0}^{2n - 1} e^{(2\pi i)(st+js)/2n}) \newline &= \sum_{t=0}^{2n - 1} c_t(\sum_{s=0}^{2n - 1} \omega_{t+j,2n}^s) \end{align}
In class
Finite Field $\mathbb{Z}_p$, where p is a prime $(\mathbb{Z}_p, +, 0)$, $(\mathbb{Z}_p^*, *, 1)$
$\mathbb{Z}_p^* = \{1, …, p-1\} = \{g^i$ and $p | i = 0, …, p-2\}$
$\forall$ prime p $\exists g$
$\mathbb{Z}_{257}^* = \{2^i | i = 0, …255\}$
$|\mathbb{Z}_{257}^*| = 256 = 2^8$
$o(g) = min\{i>0| g^i$ and $ p\}\bigg||\mathbb{Z}_p^*| = 256$