Convex Optimization
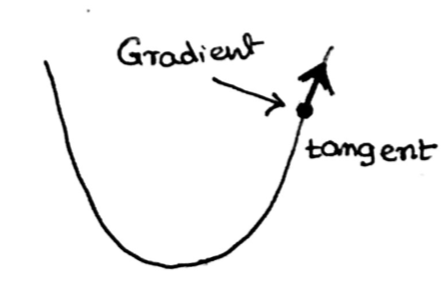
Gradient && Hessian
The gradient of a f, d x 1, can be represented as follow
$$ \nabla f(x) = \begin{bmatrix} \frac {\partial f(x)} {\partial x_1} \newline …\newline \frac {\partial f(x)} {\partial x_d} \end{bmatrix} $$
and the Hessian, d x d, can be represented as
$$ \nabla^2 f(x) = \begin{bmatrix} \frac {\partial^2 f(x)} {\partial x_1^2} & \frac {\partial^2 f(x)} {\partial x_1x_2} & \frac {\partial^2 f(x)} {\partial x_1x_d} \newline … & … & …\newline \frac {\partial^2 f(x)} {\partial x_d^2} & \frac {\partial^2 f(x)} {\partial x_dx_2} & \frac {\partial^2 f(x)} {\partial x_dx_d} \newline \end{bmatrix} $$
With flatter graph, the Hessian will approach 0, lower matrix norm.
Local Optimimality
Suppose we have $w^*$, what determine $w^*$ a optimal solution?
1-d
Necessary condition: $f’(w^*) = 0, f”(w^*) \geq 0$
Sufficient condition: $f’(w^*) = 0, f”(w^*) \gt 0$
d-dimension
Necessary condition: $f’(w^*) = 0, \nabla(w^*)$ is positive semi definite
Sufficient condition: $f’(w^*) = 0, \nabla^2(w^*)$ is positive definite
Positive Semi Definite (PSD)
A dxd matrix A is positive semi definite if for all dx1 vector z, $z^TAz \geq 0$
A dxd matrix A is positive definite if for all dx1 vector z, $z^TAz \gt 0$
Convexity
A set S $\subseteq R^d$ if for any x, y $\in$ S and $0 \leq \lambda \leq 1$, that $(\lambda x + (1 -\lambda)y) \in S$ as well.
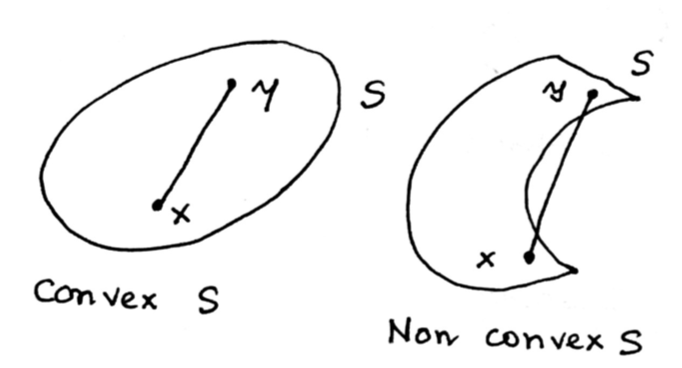
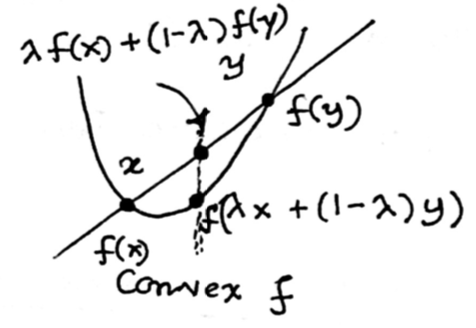
Analogously, a function $f: R^d \rightarrow R$ is convex if for any x, y in domian and $0 \leq \lambda \leq 1$, $f(\lambda x + (1 -\lambda)y) \leq \lambda f(x) + (1 - \lambda)f(x)$.
Properties of Convex Functions
- if f is differentiable, then for any y, x, then $f(y) - f(x) \geq \nabla f(x)^T(y-x)$
- “f lies above the gradient”
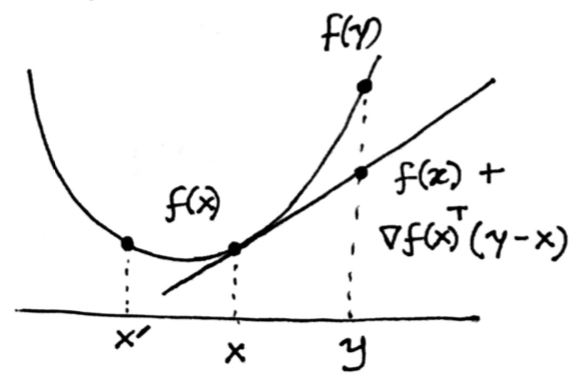
- “f lies above the gradient”
- if f is doubly differentiable at x, then $\nabla f(x)^2$ is PSD.
Why convex functions are special:
- local minimum are global minimum
- optimal solutions are all connected
- you can always go “downhill” to optimal solution
Examples:
- linear regression
- $f(w) = ||y-Xw||^2 = (y - Xw)^T(y - Xw)$
- $\nabla f(w) = -2X^Ty + 2X^TXw$
- $\nabla^2 f(w) = X^TX$, which is PSD
- logistic regression
- $f(w) = \sum_{i=1}^n \ln (1 + e^{-y^{(i)}(w^T \cdot x^{(i)})})$
- $\nabla f(w) = \sum_{i=1}^n \frac{-y^{(i)}x^{(i)}}{1 + e^{y^{(i)}(w^T \cdot x^{(i)})}}$
- $\nabla^2 f(w) = \sum_{i=1}^n \frac{-y^{(i)2}x^{(i)}x^{(i)T}}{(1 + e^{y^{(i)}(w^T \cdot x^{(i)})})(1 + e^{-y^{(i)}(w^T \cdot x^{(i)})})}$, which is PSD again