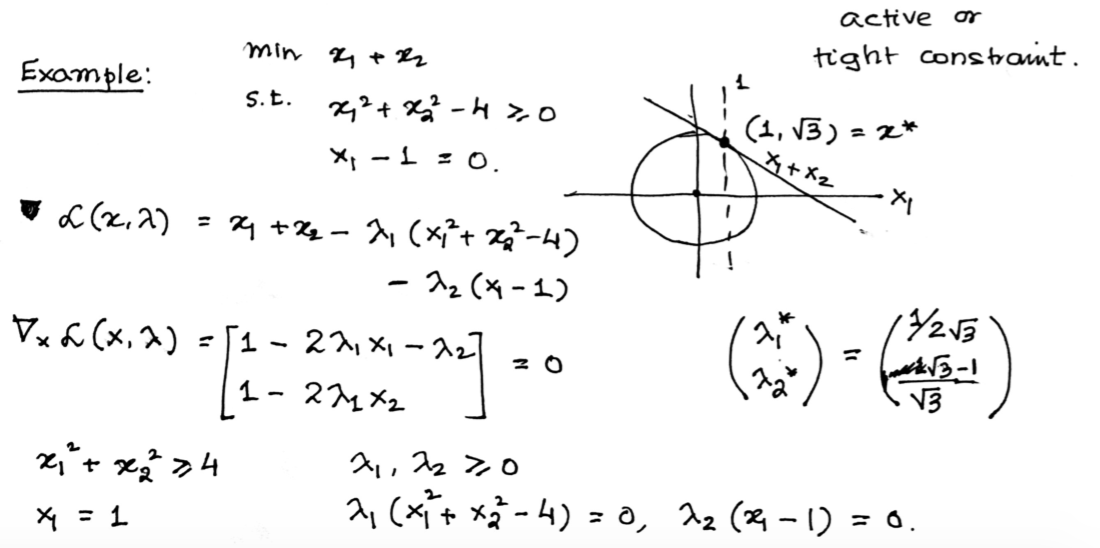Constrained Optimization

Constrained Optimization

$$\min_{x \in R^n} f(x)$$

subject to: $$c_i (x) = 0, i \in E \text{(equality constraints)}$$ $$c_i (x) \geq 0, i \in I \text{(inequality constraints)}$$

Feasible Set $\Omega = { x_i | c_i(x) = 0, i \in E \text{ and } c_i(x) \geq 0, i \in I}$.

Case 1

$\min_{x \in R^n} f(x)$ subject to $c_1 (x) = 0$

x is local minimum if x + s $\notin \Omega$ or f(x+s) $\geq$ f(x).

Now, assume the opposite. Suppose s is a small step, $c_1(x+s) = c_1(x)$ and $f(x+s) < f(x)$

Using Taylor Series Expansion:

$$c_1(x+s) \approx c_1(x) + \nabla c_1(x)^T s = 0$$

So

$$\nabla c_1(x)^T s = 0$$

Also, since $f(x+s) < f(x)$, then

$$0 > f(x+s) - f(x) \approx \nabla f(x)^T s$$

Therefore, $\exists s$ when

$$\begin{align} \nabla c_1(x)^T s &= 0 \newline \nabla f(x)^T s &< 0 \end{align}$$

However, this is not possible when $\nabla f(x) = \lambda \nabla c(x)$. If $\nabla f(x)$ and $\nabla c(x)$ lie parallely, s will be perpendicular to $\nabla f(x)$ as well, making dot product 0 instead of <0.

$\therefore$ the optimality condition are $\nabla f(x) = \lambda \nabla c(x)$.

Case 2

Subcase 2.a

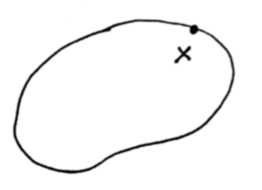
$\min_{x \in R^n} f(x)$ subject to $c_1 (x) \geq 0$

Suppose $\exists$ a small step s, s.t. $c_1(x+s) \geq 0$ and $f(x+s) < f(x)$.

Then

$$c_1(x+s) \approx c_1(x) + \nabla c_1(x)^T s \geq 0 \text{ (a)}$$

$$f(x+s) = f(x) + \nabla f(x)^T s < f(x) \text{ (b)}$$

Any s satisfy the equation (a), and $\exists$ s that satisfy (b) unless $\nabla f(x) = 0$.

$\therefore$ optimality conditions: $\nabla f(x) = 0, c_1(x) > 0$.

Subcase 2.b

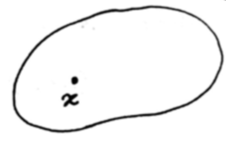
$c_1(x) = 0$

If x is not local optimal, then $\exists$ s that $c_1(x+s) \geq 0$ and $f(x+s) < f(x)$.

Again by Taylor series expandsion

$$c_1(x+s) \approx c_1(x) + \nabla c_1(x)^T s \geq 0 \text{ (a)}$$

$$f(x+s) = f(x) + \nabla f(x)^T s < f(x) \text{ (b)}$$

Because $c_1(x) = 0$, then we have

$$\nabla c_1(x)^T s \geq 0 \text{ (a)}$$

$$\nabla f(x)^T s < 0 \text{ (b)}$$

$\exists$ no s that satisfy both a and b iff $\nabla f(x) = \lambda \nabla c_1(x)$ for $\lambda \geq 0$

The Lagrangian function:

$$L(x, \lambda) = f(x) - \sum_{i \in \epsilon \cup I} \lambda_i c_i(x)$$

where $\lambda$ is called Lagrangian variable.

Karush-Kahn-Tucker (KKT) Conditions

At a local solution $x^* $, under some conditions, $\exists$ a Lagrange multiplier $\lambda^* $ s.t.

$$\begin{align} \nabla L(x^*, \lambda^*) &= 0 \newline c_i(x^*) &= 0, \forall i \in E \newline c_i(x^*) &\geq 0, \forall i \in I \newline \lambda_i^* &\geq 0, \forall i \in I \newline \lambda_i c_i(x^*) &= 0, \forall i \in E \cap I \newline \end{align}$$

The last is called complementary conditions (either $\lambda_i = 0$ or $c_i(x^*) = 0$ when $c_i(x^*) > 0$) based on rule 3 and 2.

Example