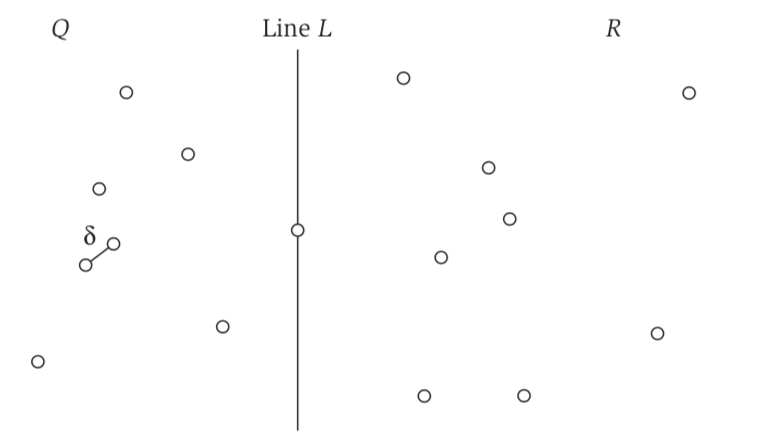
Closest Point
Problem
Given n points in the plane, find the pair that is closest together.
Brute force takes $O(n^2)$.
Algorithm
Let’s $d(p_i, p_j)$ = Euclidean distance.
In 1-d, we can simply sort points and compute the distance with the next point, we then have complexity of O(nlogn). In 2-d, we can’t applied the same thing.
We will use divide and conquer. We find the closest pair in the left and closest pair in the right, and hoping to get it in linear time.
We sort the point by x then by y in increasing order, producing list $P_x$ and $P_y$.
We then split the data into $Q_x$ and $R_x$ according to $P_x$, and $Q_y$ and $R_y$ according to $P_y$.