CSE250 Proj2

Coordinate Descent

(a) In this project I compared different methods using different approaches. Besides the random coordinate descent (RCD), I implemented two ways to choose the coordinate: cyclic coordinate descent method(CCD) and greatest coordinate descent method (GCD). CCD updates the coordinate in cycle and GCD update the coordinate with greatest derivative.¹

(b) For every iteration, the coordinate, i, being picked will be updated with below methods.

Method 1 (Minimize Loss Function)

$$w_{i,t+1} = \text{argmin}_{w_j,t} Loss(w)$$

Method 2

$$w_{i,t+1} = w_{i,t} - \eta \frac{\partial L}{\partial w_i}$$

Let’s denote method 1 with -fmin and method 2 with -derivate.

Pseudocode

CCD()

1. Initialize w = array of 0’s
2. Let k = number of features
3. Until converged or max iterations reach
   • for i = 1 to k
     • $w_i$ = run method 1 or method 2 while fixed other $w_k$

GCD()

1. Initialize w = array of 0’s
2. Let k = number of features
3. Until converged or max iterations reach
   • maxDerivative = 0
   • j = -1
   • for i = 1 to k
     • if abs($\frac{\partial L}{\partial w_i}$) > maxDerivative
       • maxDerivative = $\frac{\partial L}{\partial w_i}$
       • j = i
   • $w_j$ = run method 1 or method 2 while fixed other $w_k$

RCD()

1. Initialize w = array of 0’s
2. Let k = number of features
3. Until converged or max iterations reach
   • i = choose a random coordinate from range of k
   • $w_i$ = run method 1 or method 2 while fixed other $w_k$

Convergence

In order to converge, the cost function needs to be smooth and convex. It needs to be first order differential in all dimensions as we are updating the all the dimensions. If above requirements are satisfied, it was proved by Luo and Tseng that, the coordinate descent method will converge asymptotically.²

Experimental Results

I used sklearn LogisticRegression model to compute the coefficient and the loss function.

The coefficient w is

\begin{bmatrix} 6.3221 \newline 2.4985 \newline 5.1498 \newline -6.5362 \newline 0.6928 \newline 0.4479 \newline 2.1750 \newline -0.7837 \newline -0.6253 \newline 1.6413 \newline -0.2698 \newline 2.5113 \newline 8.4829 \newline \end{bmatrix}

The loss $L^*$ = 0.0126.

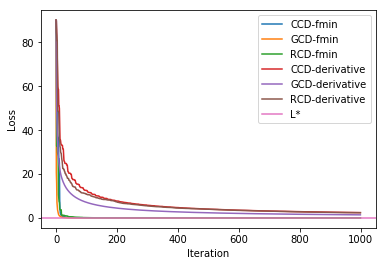
By running the CCD, GCD, and RCD with -fmin and -derivative methods, the above graph is generated. As one can see, all methods approach $L^*$ asymptotically.²

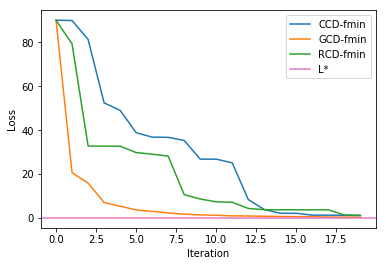
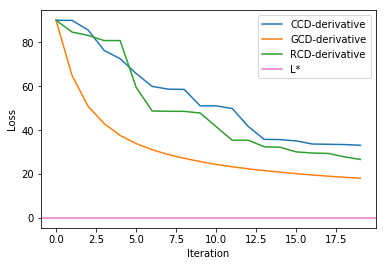
In both methods, the GCD performed best as we can see from the above graph. This is expected since GCD picked the coordinate with greatest partial derivative which will move down the loss function the greatest. But, GCD is more computationally expensive due to finding the derivative of all feature spaces. On the other hand, it is interesting to see that the RCD performed better than CCD. This phenomenon was actually observed by many data scientists as well.³ It was shown that only if the Hessian is 2-cyclic matrix or M matrix, CCD could converge 2 times faster than RCD .³ But Asymptotically, there should not be any different between RCD and CCD since each coordinate will be updated about same number of times.

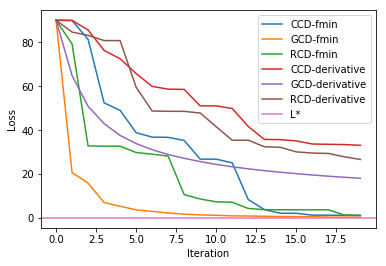
Comparing fmin method and derivative method, we can see fmin method converge faster. This is because fmin solve the $w_i$ the minimize the loss directly instead of taking few steps to go there. Therefore all the approaches with derivative method run behind the fmin methods. Although fmin is quicker, we also spend extra computation power to find the $w_i$ that minimize the loss function. This may not be feasible if we have large dimensions of features. Furthermore, all methods converge to $L^*$ eventually we might be better of just use the derivative methods.

Critical Evaluation

There are many ways to improve the coordinate descent algorithm. Instead of single coordinate descent, we can update a block of coordinates⁴. The block coordinate descent is proved to converge as well.⁵ There is also Gauss-Southwell rule that select the coordinate which maximize the gradient of the loss function, or Gauss-Southwell-Lipschitz rule that maximize the gradient of loss function over squared root of Lipschitzconstant, where both of them are proved to be faster than RCD.⁶

Sparse Coordinate Descent

We need to introduce the L1 regularizer. The LASSO regularization is very helpful in feature selection. The Loss function will become following

$$L(w) = \sum_{i=1}^n \ln(1 + exp(-y^{(i)}(w \cdot x^{(i)}))) + \lambda ||w||_1$$

When we take derivative we need to take L1 norm into consideration.

\begin{bmatrix} 3.3101 \newline 1.1142 \newline 2.3264 \newline -2.829 \newline 0. \newline 0. \newline 1.0179 \newline 0. \newline 0. \newline 0.749 \newline9 -0.2244 \newline 1.1700 \newline 4.7748 \newline \end{bmatrix}

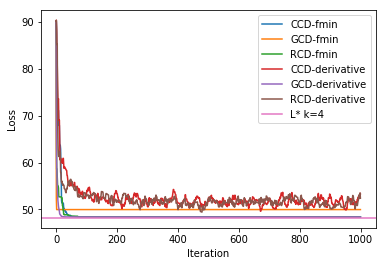
We observe with L1 regularizer, CCD-derivative and RCD-derivative start to fluctuate through out the iterations. The loss value also increase after we introduce the regularizer.

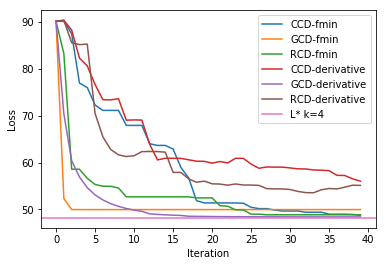
When we zoom in to the first few iterations, we still see that GCD converged the fastest.