Project 1

1. Prototype Selection

Divide data into ${S_1, S_2, …, S_c}$, where c = number of labels. For each dataset $S_i$, I select M/c points as new training set for that label, which are the centroids by running k-means clustering algorithm.

My idea was to capture as many distinct types in for each label and meanwhile reduce the noise by selecting only the center of the each type.

2. Pseudocode

create knnWrapper(dataX, dataY, neighbor, protype_num)

  • dataX = training data for X
  • dataY = label data for corresponding X
  • neighbor = number of closest neighbors picked to decide the query point
  • prototype_num = desired final data size

model = run knnWrapper(dataX, dataY, 1, M)

model.predict(query)

Detailed Implementation for knnWrapper():

$trainX = \emptyset$
$trainy = \emptyset$
labels = extra distinct labels from dataY
$data$ = group dataX by its label

for label in labels

  • centroids = find_k_means_clusters(data[label], M / C)
  • trainX = trainX + centroids
  • trainy append label M/C times

return knn(trainX, trainy, neighbor)

3. Experimental Results

The margin of error can be calculated according to 1 $$ME = Z\sqrt{\frac{p(1 -p)}{n}}$$ where

  • Z is Z-value from z-table 2, 1.96 chosen for 95% confidence interval
  • p = proportion mean of sample
  • n = sample size.

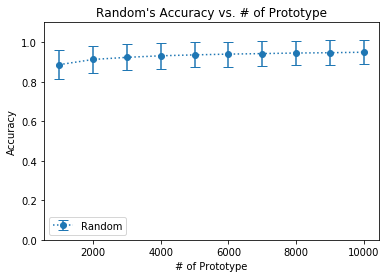
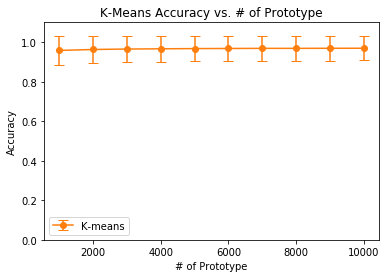
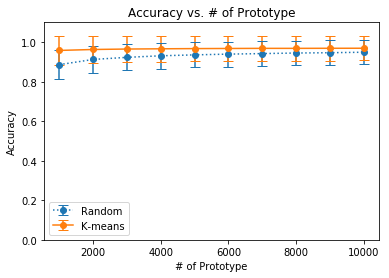
The following plots are for random selection and k-means: Random's Accuracy vs Prototye K-mean's Accuracy vs Prototye Accuracy vs Prototye

Accuracy for Random vs K-Means PS

Num of Prototype Accuracy of Random Accuracy of K-Means
1000 0.8861 $\pm$ 0.1137 0.9580 $\pm$ 0.0718
2000 0.9123 $\pm$ 0.1012 0.9628 $\pm$ 0.0678
3000 0.9230 $\pm$ 0.0954 0.9650 $\pm$ 0.0657
4000 0.9309 $\pm$ 0.0908 0.9662 $\pm$ 0.0646
5000 0.9355 $\pm$ 0.0879 0.9673 $\pm$ 0.0637
6000 0.9393 $\pm$ 0.0854 0.9679 $\pm$ 0.0631
7000 0.9420 $\pm$ 0.0836 0.9685 $\pm$ 0.0625
8000 0.9449 $\pm$ 0.0817 0.9685 $\pm$ 0.0625
9000 0.9464 $\pm$ 0.0806 0.9689 $\pm$ 0.0621
10000 0.9489 $\pm$ 0.0788 0.9691 $\pm$ 0.0619

4. Critical Evaluation

My method is a improvement to the random selection. There are many more techniques for PS, such condensation, edition, and hybrid. I would love to try some of the hybrid methods that can further improve the performance, for example Repeated Editing Fast Condensing Nearest Neighbour (RFCNN). Moreover, besides PS methods, they are approaches focusing on different aspect of problem for kNN. One aspect is looking at different dist function, such as Fast Similarity Search, Approximated Similarity Search, etc.3 Also, one can also try differnt data structure for storing the points, such as vp-tree which provides O(logn) search time.4

Image credit to sci2s 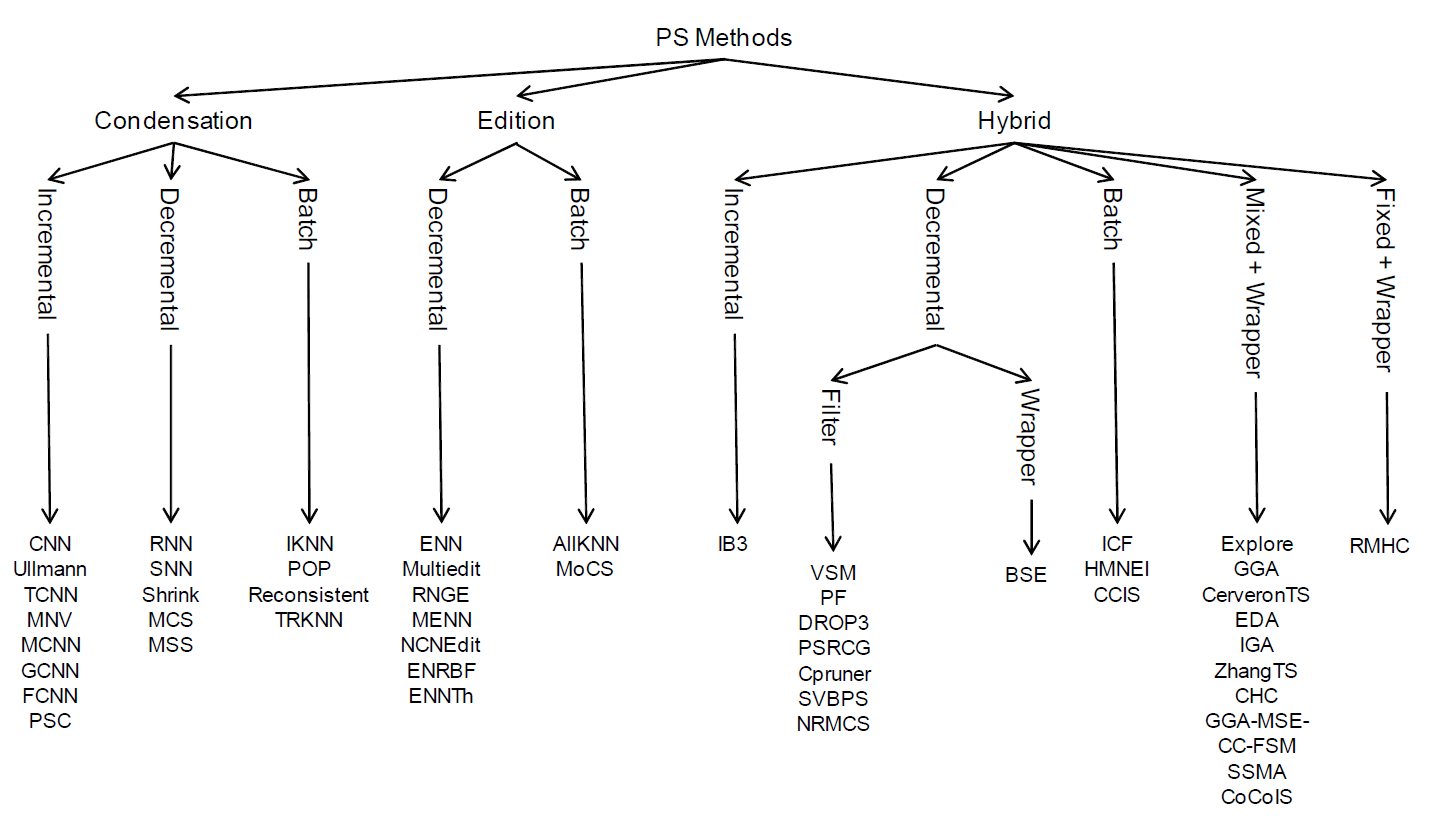PS Methods

  1. Confidence Intervals for a Single Mean or Proportion, Lisa Sullivan, Wayne LaMorte, http://sphweb.bumc.bu.edu/otlt/MPH-Modules/QuantCore/PH717_ConfidenceIntervals-OneSample/PH717_ConfidenceIntervals-OneSample_print.html [return]
  2. http://www.ltcconline.net/greenl/courses/201/estimation/smallConfLevelTable.htm [return]
  3. On the suitability of Prototype Selection methods for kNN classification with distributed data, Jose J. Valero-Mas, Jorge Calvo-Zaragoza, Juan R. Rico-Juan, https://grfia.dlsi.ua.es/repositori/grfia/pubs/341/SuitabilityPSDistributedScenarios.pdf [return]
  4. Data Structures and Algorithm for Nearest Neighbor Search in General Metric Spaces, Peter N. Yianilos, http://web.cs.iastate.edu/~honavar/nndatastructures.pdf [return]