CSE202 HW2

HW Link

Problem 1 (KT 5.2)

Idea: we will need to modify the merge-and-count function, everything else stays the same as regular inversion algorithm.

merge-and-count(A, B):

1. i = 1, j = 1, where i is pointer to A, j is pointer to B
2. count = 0, lenA = length(A), lenB = length(B)
3. sorted = {}
4. While $i \leq lenA$ and $j \leq lenB$:
   • if (A[i] $\leq$ B[j])
     • sorted = sorted + {A[i]}
     • $i \gets i + 1$
   • else
     • sorted = sorted + {B[j]}
     • $j \gets j + 1$
5. append remaining A or append remaining B to sorted
6. While $i \leq lenA$ and $j \leq lenB$:
   • if (A[i] $\leq$ 2B[j]), means no significant inversion
     • $i \gets i + 1$
   • else
     • $j \gets j + 1$
     • $count \gets count + (lenA - i + 1)$
7. return (sorted, count)

Analysis

Time Complexity

Instead of looping once for original inversion problem, we here loop twice. One for making the element sorted, and one for counting number of significant inversion. Our conquer step will take O(2n), which is still O(n), so T(n) = 2T(n/2) + O(n) still holds. Thus the overall algorithm is still $O(n\log n)$.

Space Complexity

T(n) = O(n)

\pagebreak

Problem 2

part (a)

Since there are 4 addition, 2 substractions. Assume all other operations takes negligible time and all the $B^n$ is precomputed to save time.

We have following

\begin{align} T(1) &= 1 \newline T(n) & = 3T(n / 2) + 6 \end{align}

Solving the above recurence euqaion, we got

$$T(n) = 4 \cdot 3 ^ {\log n} - 3 = 4 n ^ {\log 3} - 3$$

part (b)

ALG(A, B, n):

1. pad A and B to 2n digits
2. A = pad(A, 2n)
3. B = pad(B, 2n)
4. A = DFT(A, 2n)
5. B = DFT(B)
6. C = $A \cdot B$
7. coefficient = IDFT(C)
8. return Coefficient

pad(A, d):

1. pad the input A to desired digits

DFT(x, N, s)¹ :

1. if N = 1
   • return X
2. else
   • $X_0, … X_{N/2 - 1} \gets$ DFT(x,N/2, 2s)
   • $X_{N/2}, … X_{N -1} \gets$ DFT(x + s,N/2, 2s)
   • Full DFT Step:
   • for k = 0 to N / 2 - 1
     • $t \gets X_K$
     • $X_k \gets t + e^{\frac{2\pi i k}{N}} X_{k+N/2}$
     • $X_{k + N / 2} \gets t - e^{\frac{2\pi i k}{N}} X_{k+N/2}$
   • endFor
3. endIf

Assume that all the roots of unity is precomuted to save time. Now for DFT, the recurrent relation is $T(N) = 2T(N/2) + 2N$, which is $T(N) = 2N \log_2 N$, IDFT performs excatly the same steps in reverse, so we can treat the time complexity as same.

Since there are 3 DFT operations, and N dot operations, we have overall time complexity of

\begin{align} T(N) &= 3 \times 2N \log_2 N + N \newline T(n) &= 3 \times 2 (2n) \log_2 {2n} + 2n \newline &= 12 n \log_2 {2n} + 2n \newline &= 12 n (\log_2 2 + \log_2 n) + 2n \newline &= 14 n + 12n\log_2 n\newline \end{align}

Finally incoporating the 10 times cost to float points operations, we got

$$T(n) = 140 n + 120 n\log_2 n$$

part (c)

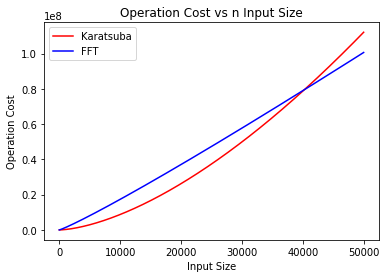
Using scipy library, I got n = 40254.58180453, So if n >= 40255, FFT outperforms Karatsuba.

Problem 3

Algorithm 1:

Basic Idea: for each vertex v, find the two longest paths orginate from v.

We need to create a adjacency matrix or neighbor list for each v.

Alg(T):

• Let adj = {neighbors[i], where i = 1 to n} from buildAdjMatrix(T)
• Let diameter = 0
• Let visited = {}
• for v in V
  • add vertex to be visited to avoid next node travel back
  • loop through neighbors[v] and calculate the distance
  • $maxDist_v$ = sum of two longest paths (or just one for 1 neighbor)
  • diameter = max($diameter$, $maxDist_v$)
• return diameter

Complexity

Time Complexity

Building adjacency matrix takes O(n). For each loop, we will take O(n) to visit possibly all the vertices. By looping n times, we have $O(n^2)$. Overall we have $O(n^2 + n) = O(n^2)$

Space Complexity

We will at most store 2n vertices in adj matrix and n status in visited. So the overall space is O(n).

Where

• V = vertices of graph
• T = graph
• m = number of edges
• n = number of vertices

Algorithm 2 (Improved Algorithm):

Idea: we have done a lot of repeated work to find the disitance between different iterations. We can see that the maximum diameter should be either on subtrees of current vertex or span across different subtree (including current vertex). We can recursively split the problem into k subgroups and perform the calculation.

k = number of neighbors for each vertex, which can be different for diffrent vertex.

Alg(T):

• Let adj = {neighbors[i], where i = 1 to n} from buildAdjMatrix(T)
• Let global variable diameter = 0
• Let visited = {}
• Let x = an abitary vertex in V.
• DFS(x, adj, visited)
• return diameter

DFS(x, adj, visited):

• if visited[x] return
• Let longestDist = 0, secondLongestDist = 0
• set x to be visited
• for neighbor in adj[x]:
  • dist = DFS(neighbor)
  • if dist > longestDist
    • longestDist $\gets$ dist, secondLongestDist $\gets$ longestDist
  • else if dist > secondLongestDist
    • secondLongestDist $\gets$ dist
• diameter = max (longestDist + secondLongestDist, diameter)
• return longestDist

Complexity

Time Complexity

Building adjacency matrix takes O(n). For the n loops, we basically split the vertices into groups of neighbors. Let’s assume without loss of generality that at each vertex we split into k groups, so T(n) = kT(n/k) + O(1). Based on master theorem, this is O(n) complexity. Alternatively, we can see that the algorithm visit each node exactly 1 time. Overall we have $O(n + n) = O(n)$

Space Complexity

Same as above, so space complexity is O(n).

Proof

Claim 1: The algorithm cover all the paths possible and return the diameter of the tree.

Assume the contary, the return value is not the diameter, which means there is a path has longer distance than diameter. Let’s call this path $P_{uv}$. Let’s assume z is the root vertext of this path. There are two possible cases

• our original solution contains z
• our original solution doesn’t contains z

Let’s define our original solution to be $P_{xy}$.

If our original solution contains z, then at the step when we try to find the two longest paths, we would’ve pick $P_{uv}$. We ended up choose our $P_{xy}$ because $P_{xz}$ and $P_{yz}$ is the two longest path, so $P_{uz}$ < ($P_{xz}$, $P_{yz}$) and $P_{vz}$ < ($P_{xz}$, $P_{yz}$), so $P_{uz} + P_{zv} < P_{xz} + P_{zy}$. So $P_{uv}$ can’t be the diameter.

If our original solution doesn’t contain z, this happens in the another vertex a, where $a \neq z$. However, if the $P_{uv}$ is the true diameter, the diameter value will not be replaced by the $P_{cd}$ that goes through vertex a. Therefore $P_{uv}$ cannot be the true diameter.

Claim 2: The longest path lies between two leaf nodes.

If this is not the case, we can always extend the path with additional nodes to make it longer.

Problem 4

Idea: for each book we can either start a new shelf by itself and append to the exisiting shelf. SO we define a dp array BEST, where BEST[i] stores the best height for stacking the the books from i to n. Thus, we start from the last book $b_n$ to $b_1$.

Assuming each book’s width is smaller than W, otherwise there is no solution at all.

Algorithm

Alg(h, t)

1. Let BEST = array of size n
2. BEST[n] = $h_n$
3. for i = n - 1 to 1
   • currentShelfHeight = $h_i$
   • currentWidth = $w_i$
   • bestSoFar = $\infty$
   • for j = i + 1 to n
     • currentWidth $\gets$ currentWidth + $t_j$
     • if currentWidth > W, break the loop
     • currentShelfHeight = max(currentShelfHeight, $h_j$)
     • if BEST[j] + currentShelfHeight < bestSoFar
       • bestSoFar $\gets$ BEST[j] + currentShelfHeight
   • BEST[i] = bestSoFar
4. return BEST[1]

Complexity

Time Complexity

T(n) = O($n^2$), double for loops and each loops takes around n times.

Space Complexity

T(n) = O(n), only auxiliary array of size n is used.