CSE202 HW1
Problem 1 (KT 4.2a)
YES. T is still the MST for new instance.
Proof by contraction
- Assume original MST is T and new MST is T’
- $T \neq T’$, at least one edge is different
- $\exists$ $e_1 \in T$ and $e_2 \in T’$, whose $cost(e_1) < cost(e_2)$ and $cost^2(e_1) > cost^2(e_2)$
- However, the above mathematical expression doesn’t hold
Problem 2 (KT 4.2b)
No. The P is no longer the shortest path for new instance.
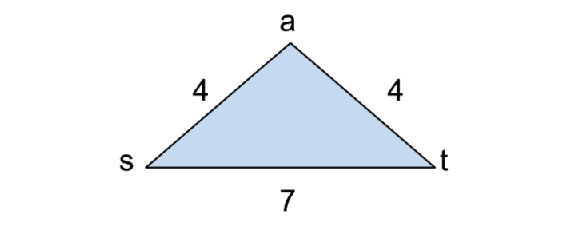 As we can see, in the Dijkastra’s algorithm, the edge e(s,t) is the shortest path with cost = 7. After squaring the cost, there is a shortest path P’ = s -> a -> t with cost of 32 < cost(P) = 49.
As we can see, in the Dijkastra’s algorithm, the edge e(s,t) is the shortest path with cost = 7. After squaring the cost, there is a shortest path P’ = s -> a -> t with cost of 32 < cost(P) = 49.
Problem 3 (KT 17)
Algorithm:
- Let $I = \{I_1, I_2, …, I_n\}$ and best = 0
- Sort I based on the finish time, f(i)
- for i in n
- let $R = I \setminus \{I_j | i \neq j$ and $I_i \cap I_j \neq \emptyset\}$
- let num_of_jobs = perfome regular interval scheduling algorithm on R
- best = max(best, num_of_jobs + 1)
Time complexity anaylysis:
Step 2, sorting takes $O(nlogn)$.
Step 3, the for loops takes $O(n^2)$ overall, since looping through intervals takes O(n), pruning + regular interval scheduling algorithm takes O(n)
So time complexity = $O(nlogn + n^2)$ = $O(n^2)$.
Space complexity analysis:
We don’t use any extra space, so space complexity = O(1).
Proof of Optimality:
Claim:
The algorithm above provides the optimal solution.
Proof:
Let’s say the optimal solution is S*, which contains a $I_i$. Since above algorithm is brute force algorithm go through each job, we are guranteed that when are checing the optimal number for $I_i$ the number is updated.
Problem 4
Algorithm:
Let $J = \{J_1, J_2, …, J_n\}$, where $J_i$ contains $c_i$ and $p_i$
Let $C = C_0$
while k > 0
- find project x, which $c_x <= C$ and $p_x$ is max
- if $x = \emptyset$ break
- $C \gets C + p_x$
- $k \gets k - 1$
Proof of Optimality:
Claim:
The gready algorithm above produces the optimal capital, C*.
Proof:
Let’s say in loop i, we have capital C, we choose a different $J_y$. Since our algorithm picks $J_x$, it implies that $p_y \leq p_x$ and also new capital $C’ \leq C$. In the next round, when we consider all the jobs whose cost are smaller than the current capital, the new heap $H’ \subseteq H$, which shows that our algorithm stays ahead in every step.
Time Complexity:
T = O(kn), if k = n we have $T = O(n^2)$.
Space Complexity:
No extra space, so space complexity = O(1).
Improved Algorithm:
Let $J = \{J_1, J_2, …, J_n\}$, where $J_i$ contains $c_i$ and $p_i$, then sort J based on $c_i$
Let H = maxheap sorted on J’s profit
Let $C = C_0$
Let z = 1, pointer for J
loop add_job:
while $z \leq n$ and $c_z \leq C$
- push $J_z$ to H
- $z \gets z + 1$
excute loop add_job
while k > 0 and H is not empty
- $J_x$ = extractMax from H
- $C \gets C + p_x$
- execute loop add_job
- $k \gets k - 1$
Time Complexity:
- Sorting takes O(nlogn).
- Extractmax takes retrieval + deletion = O(1) + O(logn) = O(logn). For k loops, complexity = O(klogn).
- The add_job inserts n jobs, each insertion takes O(logi) where i = size of heap. So $\sum_i^n log(i) = O(nlogn)$.
- So overall = O(nlogn + klogn) = O(nlogn), since $k \leq n$
Space Complexity:
O(n) for storing all the projects in the heap.
Problem 5
Algorithm:
sort $T = \{t_1, t_2, …, t_n\}$ in decreasing order
sort $W = \{w_1, w_2, …, w_n\}$ in decreasing order
Let i = 1, pointer for T
Let j = 1, pointer for W
Let result = {}
while $i \leq n$
- If $t_i$ / $w_j$ $\leq D$
- $i \gets i + 1$
- $j \gets j + 1$
- result + {i, j}
- else
- $i \gets i + 1$
Proof of Optimality:
Claim:
The above algorithm produces the optimal assignment, R.
Proof:
Assume there is a better assignment R’, where |R’| > |R|.
This can happen by either case:
- R’ = R + {i, j}
- R’ have different arrangement of pairs that vacant a machine to take on another task, resulting more tasks to be taken
For case 1, let’s say in step i, our algorithm rejects the task because $t_i$ / $w_j$ $\gt D$, but R’ takes this pair {i, j}. This will be a violation to the requirement since this machine can’t complete the task on time.
For case 2, the only way that R’ and R will take on different arrangement is when R decides to take the pair {i, j} but R’ decides to ignore the $t_i$. This have vacated the $w_j$, we now have |R| > |R’|. In the next round, $w_j$ can try to take the $t_{i+1}$, making $|R’| \gets |R’| + 1$ or 0. In the meantime, R could either take the new pair {i+1, j+1} or rejects. In the best case scenario, $|R’| \gets |R’| + 1$, while |R| stays, making |R’| = |R| in this round. However, in every round, |R| $\geq$ |R’|.